Question

How do you find the area between $f\left( x \right)=\dfrac{10}{x}$, $x=0, y=2, y=10$?

Answer 1

This type of question is based on the concept of application of definite integral. We are given the curve $f\left( x \right)=\dfrac{10}{x}$, let us assume $y=\dfrac{10}{x}$. To find the area enclosed by both the curves, we have to find the intersection points of both the curves. Here we have been given two parallel lines $y=10$ and $y=2$. Therefore, we can integrate with respect to y with 10 and 2 as the limits of the integration. The formula to find the area will be $A=\int{xdy}$ with the limits 2 and 10. To find $x$, we have to cross multiply $y=\dfrac{10}{x}$ so that we get $x=\dfrac{10}{y}$. Integrate and do necessary calculations to find the area enclosed by these curves.

Complete step by step solution:
According to the question, we are asked to find the area $f\left( x \right)=\dfrac{10}{x}$, $x=0, y=2, y=10$.
We have been given the curves are $f\left( x \right)=\dfrac{10}{x}$, $x=0, y=2, y=10$.
First, we have to consider $f\left( x \right)=\dfrac{10}{x}$.
Consider $f(x)=y$. therefore, we get $y=\dfrac{10}{x}$.
Now, let us plot the graph for the curves $y=\dfrac{10}{x}$, $x=0, y=2$ and $y=10$.
We get

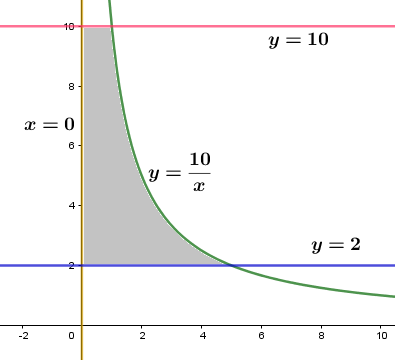
Here, the shaded region $s$ the required area.
Let us integrate with respect to y since the limits of $y$ are $2$ and $10$.
Therefore, we get that the area enclosed by $y=\dfrac{10}{x}$ over the limits $y=2$ to $y=10$ is
$A=\int\limits_{2}^{10}{xdy}$
But, we have to find the value of x with respect to $y$.
Therefore, we have to cross-multiply $y=\dfrac{10}{x}$ to get the value of $x$ in terms of $y$.
We know that, if $\dfrac{a}{b}=c$ then $\dfrac{a}{c}=b$. Using this method of cross multiplication, we get
$\Rightarrow x=\dfrac{10}{y}$
Thus, the area enclosed by the curves is
$A=\int\limits_{2}^{10}{\dfrac{10}{y}dy}$
Since 10 is a constant, we can take $10$ out of the integration.
$\Rightarrow A=10\int\limits_{2}^{10}{\dfrac{1}{y}dy}$
We know that $\int{\dfrac{1}{x}}dx=\log x$. On integrating $\dfrac{1}{y}$ with respect to $y$, we get
$A=10\left[ \log y \right]_{2}^{10}$
On substituting the limits to the variable $y$, we get
$A=10\left[ \log 10-\log 2 \right]$
We know that $\log a-\log b=\log \left( \dfrac{a}{b} \right)$. Using this property of integration, we get
$A=10\left[ \log \left( \dfrac{10}{2} \right) \right]$
We can write the expression as $A=10\left[ \log \left( \dfrac{2\times 5}{2} \right) \right]$.
On cancelling the common term 2 from the numerator and denominator of the logarithmic function, we get
$A=10\left[ \log 5 \right]$
$\therefore A=10\log 5$ square units.
Therefore, the area between $f\left( x \right)=\dfrac{10}{x}$, $x=0, y=2, y=10$ is $10 log 5$ square. units.

Note: We have to use definite integrals to solve these types of questions. We have to know the properties of logarithm to simplify the final answer. Avoid calculation mistakes based on sign convention. We should not forget to put units after finding the area without which the answer is incomplete.