Question

How do you find the area and perimeter of parallelogram with vertices at points $\left( { - 6, - 5} \right)$,$\left( { - 2,4} \right)$,$\left( {5,4} \right)$and$\left( {1, - 5} \right)$?

Answer 1

In this question we have to find the area and perimeter of parallelogram, we use the fact that the diagonal of a parallelogram divides the parallelogram into two equal parts, so area of parallelogram is twice the area of the triangle, so to find the area of triangle we will use the formula $\dfrac{1}{2}\left| {\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]} \right|$, and for the perimeter we will make use of the distance formula which is given by $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$ and find the length of the sides of the parallelogram, and we know that the perimeter is the sum of all sides of the parallelogram, so by adding the lengths of the sides we will get the perimeter of the parallelogram.

Complete step-by-step answer:
Let the coordinates of the parallelogram be A$\left( { - 6, - 5} \right)$, B$\left( { - 2,4} \right)$, C$\left( {5,4} \right)$ and D $\left( {1, - 5} \right)$,
Using the distance formula which is given by,$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$, we will find the length of the sides of the parallelogram using the coordinates.
Now substituting the coordinates in the formula we get,
$AB = \sqrt {{{\left( { - 2 - ( - 6)} \right)}^2} + \left( {4 - {{( - 5)}^2}} \right)}$,
Now simplifying we get,
$\Rightarrow AB = \sqrt {{{\left( { - 2 + 6} \right)}^2} + {{\left( {4 + 5} \right)}^2}}$,
Now adding the expression to simplify we get,
$\Rightarrow AB = \sqrt {{{\left( 4 \right)}^2} + {{\left( 9 \right)}^2}}$,
Now further simplifying we get,
$\Rightarrow AB = \sqrt {16 + 81} = \sqrt {97}$,
Now finding the length of the side BC, we get,
$BC = \sqrt {{{\left( {5 - ( - 2)} \right)}^2} + \left( {4 - 4{)^2}} \right)}$,
Now simplifying we get,
$\Rightarrow BC = \sqrt {{{\left( {5 + 2} \right)}^2} + {{\left( 0 \right)}^2}}$,
Now adding the expression to simplify we get,
$\Rightarrow BC = \sqrt {{{\left( 7 \right)}^2}}$,
Now further simplifying we get,
$\Rightarrow BC = 7$,
Now finding the length of the side CD, we get,
$CD = \sqrt {{{\left( {1 - (5)} \right)}^2} + \left( { - 5 - 4{)^2}} \right)}$,
Now simplifying we get,
$CD = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 9} \right)}^2}}$,
Now adding the expression to simplify we get,
$\Rightarrow CD = \sqrt {16 + 81}$,
Now further simplifying we get,
$\Rightarrow CD = \sqrt {97}$,
Now finding the length of the side AD, we get,
$AD = \sqrt {{{\left( {1 - ( - 6)} \right)}^2} + {{\left( { - 5 - ( - 5)} \right)}^2}}$,
Now simplifying we get,
$AD = \sqrt {{{\left( {1 + 6} \right)}^2} + {{\left( { - 5 + 5} \right)}^2}}$,
Now adding the expression to simplify we get,
$\Rightarrow AD = \sqrt {{{\left( 7 \right)}^2} + {0^2}}$,
Now further simplifying we get,
$\Rightarrow AD = 7$,
Now using the diagram, we can find the area and perimeter of the parallelogram,

,

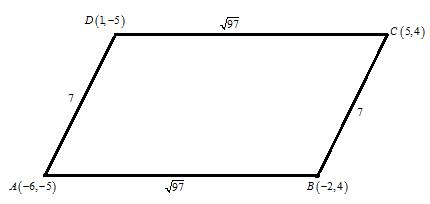We know that the area of a parallelogram is equal to the product of base and height, and the diagonal of a parallelogram divides the parallelogram into two equal parts, we can say that area of parallelogram ABCD is twice the area of the triangle ABC,
And the area of the triangle is given by formula $\dfrac{1}{2}\left| {\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]} \right|$,
So substituting the values of the coordinates in the formula, here ${x_1} = - 6$,${y_1} = - 5$,${x_2} = - 2$,{y_2} = 4$$$${x_3} = 5,and${y_3} = 4$,
Now substituting the values we get,
Area of triangle ABC=$\dfrac{1}{2}\left| {\left[ { - 6\left( {4 - 4} \right) + \left( { - 2} \right)\left( {4 - ( - 5)} \right) + 5\left( { - 5 - 4} \right)} \right]} \right|$,
Now simplifying we get,
Area of triangle ABC=$\dfrac{1}{2}\left| {\left[ { - 6\left( 0 \right) + \left( { - 2} \right)\left( {4 + 5} \right) + 5\left( { - 9} \right)} \right]} \right|$,
Now simplifying we get,
Area of triangle ABC $= \dfrac{1}{2}\left[ {0 + \left( { - 2} \right)\left( 9 \right) + 5\left( { - 9} \right)} \right]$,
Now adding for simplifying we get,
Area of triangle ABC $= \dfrac{1}{2}\left| {\left[ {0 - 18 - 45} \right]} \right|$,
Now Area of triangle ABC $= \dfrac{1}{2}\left| { - 63} \right|$,
So finally Area of triangle ABC $= 31.5$,
Now the area of the parallelogram is equal to twice the area of the triangle.
So Area of parallelogram ABCD = $2$(Area of triangle ABC),
Area of parallelogram ABCD=$2\left( {31.5} \right)$=$63$,
Now we have to find the perimeter of the parallelogram which is equal to the sum of the sides of the parallelogram, i.e.,
Perimeter of parallelogram $= AB + BC + CD + AD$,
Perimeter of parallelogram = \sqrt {97} + 7 + \sqrt {97} + 7$$$$ = 2\left( {\sqrt {97} + 7} \right),
Now the perimeter of parallelogram $= 2\left( {9.849 + 7} \right)$=2\left( {16.849} \right)$$$$ = 33.7.

$\therefore$The area of the given parallelogram is 63 square units, and the perimeter of the parallelogram is 33.7 units.

Note:
A parallelogram is a special type of quadrilateral. A parallelogram is a figure with two pairs of opposite sides that are parallel. Properties of parallelogram are:
Opposite sides are equal.
Opposite angles are equal.
Same side interior angles are supplementary.
Each diagonal divides the parallelogram into two triangles.
The diagonals bisect each other.