Question

How do you find the area and perimeter of a parallelogram with vertices at points $\left( { - 6, - 5} \right)$ , $\left( { - 2,4} \right)$ , $\left( {5,4} \right)$ and $\left( {1, - 5} \right)$ ?

Answer 1

In this question, we are given four points and we have been told that the points make a parallelogram. We have been asked to find the perimeter and the area. First, name the points and then, use distance formula to find the sides. For perimeter, just add the distances that you have found. And for the area, find the height of the parallelogram as per the corresponding base and put the values in the formula of the area of the parallelogram.

Formula used:
Distance formula: $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Area of Parallelogram: $A = b \times h$ , where $b =$ base and $h =$ height

Complete step by step answer:
Let $A = \left( { - 6, - 5} \right)$ , $B = \left( { - 2,4} \right)$ , $C = \left( {5,4} \right)$ and $D = \left( {1, - 5} \right)$ .
Let us plot these points on a graph.

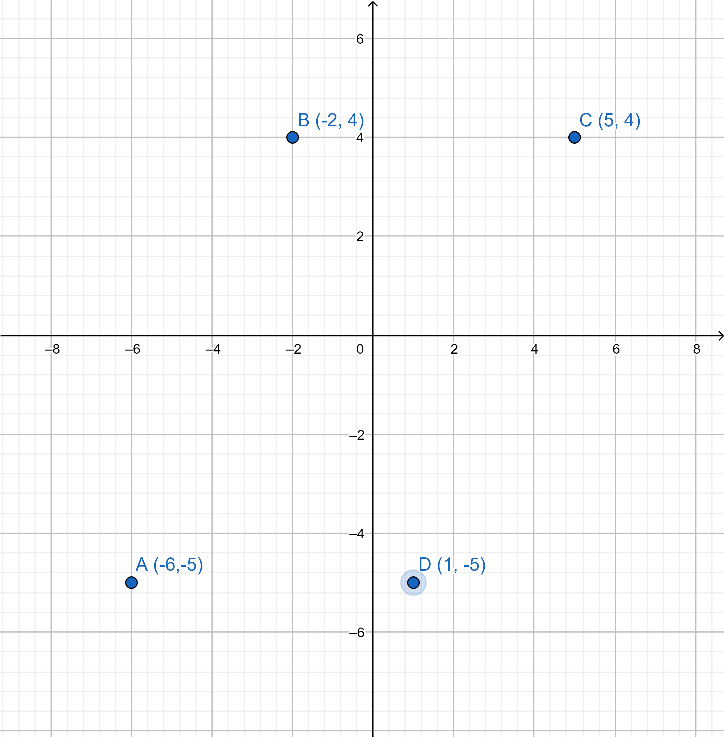
Now, we know that in a parallelogram, opposite sides are equal. So, instead of finding all the sides, we will only find two. We know that$AB = CD,BC = AD$ . So, I will find $AB$ and $BC$ only. We will use a distance formula for this purpose.
Hence, $AB = \sqrt {{{\left( { - 2 - \left( { - 6} \right)} \right)}^2} + {{\left( {4 - \left( { - 5} \right)} \right)}^2}}$
Solving it further,
$AB = \sqrt {{{\left( { - 2 + 6} \right)}^2} + {{\left( {4 + 5} \right)}^2}}$
$AB = \sqrt {{{\left( 4 \right)}^2} + {{\left( 9 \right)}^2}}$
$AB = \sqrt {16 + 81} = \sqrt {97}$
Now, $BC = \sqrt {{{\left( {5 - \left( { - 2} \right)} \right)}^2} + {{\left( {4 - 4} \right)}^2}}$
Solving it further,
$BC = \sqrt {{{\left( {5 + 2} \right)}^2}}$
$BC = \sqrt {{7^2}} = 7$
Hence,
$AB = CD = \sqrt {97} ,BC = AD = 7$
Now, we know that perimeter = sum of all sides.
We can write perimeter = $2AB + 2BC = 2\left( {AB + BC} \right)$
Putting in the values,
Perimeter = $2\left( {\sqrt {97} + 7} \right)$ units
Now, to find the area, we need to know the height of the parallelogram also. Let us take $AD$ as the base. Then, we can calculate the height from the vertex $B$ just by looking at the graph.
Height of parallelogram = distance above y-axis + distance below y-axis.
Looking from point B, height = $\left( {4 + 5} \right)$ units
Hence, height = $9$ units.
Now, area = ${\text{base }} \times {\text{ height}}$
Area = $7 \times 9 = 63{\text{ sq}}{\text{. units}}$

Note: To calculate the height, I took y-coordinates of the 2 points – point B and any point on the base AD.
Y-coordinate of point B = 4 units
Y-coordinate of any point on base AD = 5 units
When added together, we got the height = 9 units.