Question

How do you find the amplitude, period and shift for $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$?

Answer 1

We explain the main function of the given equation $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$. We take the general equation and explain the amplitude, period, and shift. Then we equate the given function $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$ with the general one and find the solution.

Complete step by step answer:
We need to find the amplitude, period, and shift for $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$.
The main function of the given equation is $\cos x$. The period of $\cos x$ is $2\pi$.
We define the general formula to explain the amplitude, period, and shift for $\cos x$.
If the $\cos x$ changes to $A\cos \left[ B\left( t+C \right) \right]+D$, the amplitude and the period becomes $\left| A \right|$ and $\dfrac{2\pi }{\left| B \right|}$.
The shift has two parts. One being phase shifting of the graph and other one being vertical shift. Phase shifting is C (positive sign means going left) and vertical shift is D.
Now we explain the things for the given $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$.
$k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)=1\times \cos \left( \dfrac{2\pi }{3}\left( t+0 \right) \right)+0$
We equate with $A\cos \left[ B\left( t+C \right) \right]+D$.
The values will be $\left| A \right|=1;\left| B \right|=\dfrac{2\pi }{3};C=D=0$. The period is $\dfrac{2\pi }{\dfrac{2\pi }{3}}=\dfrac{2\pi \times 3}{2\pi }=3$.
Therefore, the amplitude and period for $k\left( t \right)=\cos \left( 2\pi \dfrac{t}{3} \right)$ is $1,3$ respectively.
There is no vertical or phase shifting at all.

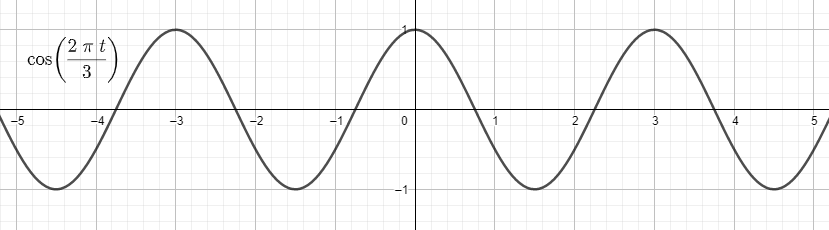
Note: Amplitude is the vertical distance from the X-axis to the highest (or lowest) point on a sin or cosine curve. Period of each generalized sine or cosine curve is the length of one complete cycle. Phase shift is the amount that the curve is shifted right or left. Amplitude and period are always a positive number. Phase shift can be of both signs.