Question

How do you find the amplitude, period, and shift for $y=3\tan x$?

Answer 1

In this problem we need to calculate the amplitude, period and shift for the given curve. To find the amplitude, period and shift of the given curve, we will write the given curve as $y=a\tan \left( bx+c \right)+d$ and compare the given equation with this equation to get the values of $a$, $b$, $c$, $d$. From these values we can write the amplitude of the curve as $a$, period of the curve as $\dfrac{\pi }{b}$ and phase shift as $-\dfrac{c}{d}$. From these formulas and the values, we will calculate the required data.

Complete step by step answer:
Given curve is $y=3\tan x$.
Converting the above equation in the form of $y=a\tan \left( bx+c \right)+d$, then we will get
$\Rightarrow y=3\tan \left( 1x+0 \right)+0$
Comparing the above equation with $y=a\tan \left( bx+c \right)+d$, then we will get
$a=3$, $b=1$, $c=0$, $d=0$.
From the above values we are going to write the following values as
Amplitude of the curve which is in the form of $y=a\tan \left( bx+c \right)+d$ is $a$, so the amplitude of the given equation $y=3\tan x$ is $3$. But for a tangent curve we don’t have the maximum value in $y$ because $\tan \left( \dfrac{\pi }{2} \right)=\infty$. So, there is no amplitude for this curve.
Period of the curve which is in the form of $y=a\tan \left( bx+c \right)+d$ is $\dfrac{\pi }{b}$, so the period of the given curve $y=3\tan x$ is $\dfrac{\pi }{1}=\pi$.
Shift of the curve which is in the form of $y=a\tan \left( bx+c \right)+d$ is $-\dfrac{c}{d}$, so the shift of the given curve $y=3\tan x$ is $-\dfrac{0}{0}=0$.
The graph of the given curve will be

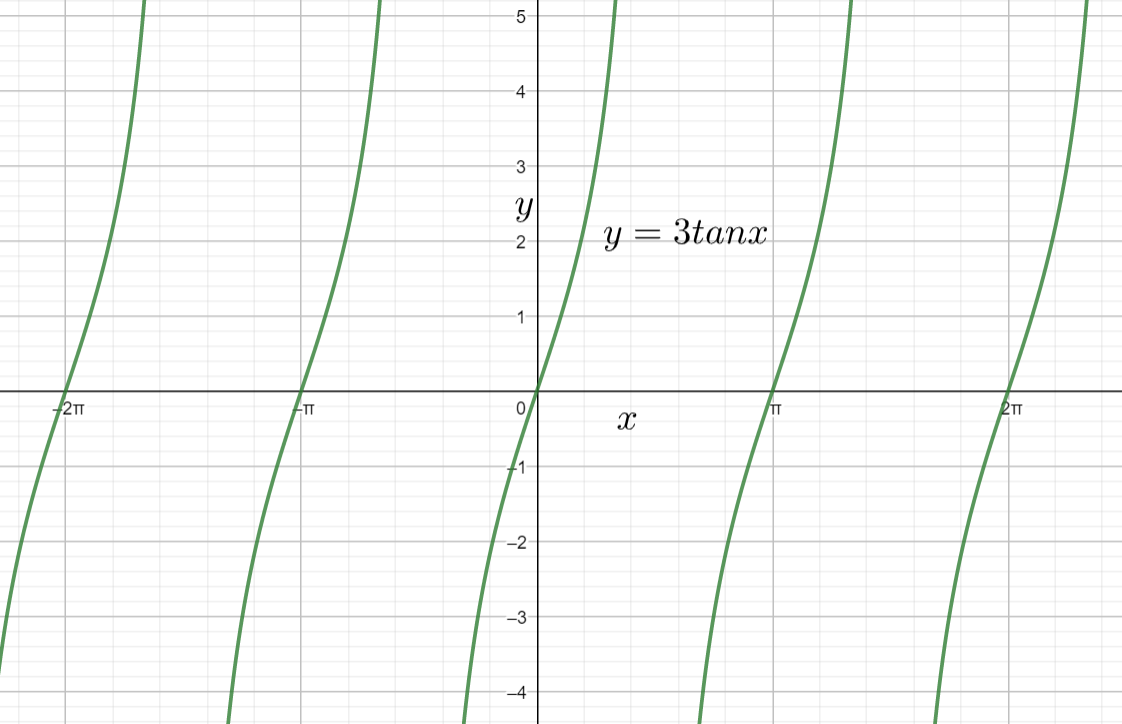
Note: We can use this method for all the trigonometric functions like $\sin$, $\cos$ etc. Except the trigonometric ratios $\tan$ and $\cot$ reaming all have maximum values that means amplitude. In the problem they don’t have asked about the vertical shift. For a curve in the form of $y=a\tan \left( bx+c \right)+d$ the vertical shift will be $d$.