Question

How do you find the amplitude and period of $y=\dfrac{1}{4}\sin x$ ?

Answer 1

Amplitude of sine function is the height from the mean of the function and it is equal to the constant multiplied to the sine function in the trigonometric expression. Period of sine function is the distance in which the function completes a full cycle (${{360}^{0}}$).

Complete answer:
Let us consider, $y=\dfrac{1}{4}\sin x$ …..equation (i).
The figure below shows plot of $y=\dfrac{1}{4}\sin x$,

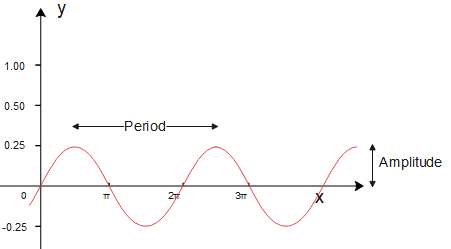
To calculate the amplitude of $y=\dfrac{1}{4}\sin x$ we compare equation to the general form of sine function,
$y=A\sin (bx+c)$ ….(ii)
Where, A is the amplitude, b is the period and c is the phase shift.
Comparing equation (i) and equation (ii), we get,
$A=\dfrac{1}{4}=0.25$
To calculate the period of $y=\dfrac{1}{4}\sin x$, in the general form of sine function equation (ii) we divide $2\pi$ by value of period (b) to get period of the trigonometric function,
Comparing equation (i) and equation (ii), we get,
$A\sin (bx+c)=\dfrac{1}{4}\sin x$
Hence,
$b=1$
Therefore, the period of $y=\dfrac{1}{4}\sin x$ is $2\pi$.

Additional Information:
The amplitude of sine function is given by the distance between two crests (i.e. the peaks or the highest point of graph) or the distance between two troughs (i.e. the lowest point on the graph). Amplitude is the coefficient of sine function. The period is the measure of a complete cycle of the function. The phase shift is shift of the function from origin to left, if phase shift is positive and to the right, if phase shift is negative.

Note:
The general expression of sine function, cosine function, tan function, etc, should be memorized to calculate the amplitude, period and phase shift of the trigonometric function. The amplitude, period and phase shift of $y=\sin x$ are 1, $2\pi$ and zero, respectively.