Question

How do you find the amplitude and period of $y=4\sin x$?

Answer 1

The characteristics of the progressive wave is defined by the general wave equation. Through which, the value of amplitude, time period and the phase angle can be known. The term y denotes the displacement and T denotes the time period. This will help you in answering this question.

Complete answer:
The wave equation has been given as the sine wave equation in general. It can be written as,
$y=A\sin (kx)........(i)$
Where A is the amplitude and k is the wavenumber.
The given equation is,
$y=4\sin x.......(ii)$
On comparing equation (i) and (ii), we can understand certain things.
The value of Amplitude has been given in the question as,
$A=4\text{ }unit$
The value of the wavenumber can be found to be as,
$k=1\text{ }unit$
Therefore the time period (T) can be calculated as follows,
$T=\dfrac{2\pi }{k}$
Substituting the values in it, we can write that,
$T=\dfrac{2\pi }{1}$
That is we can write that,
$T=2\pi$
Hence, the value of the period will be $2\pi$.

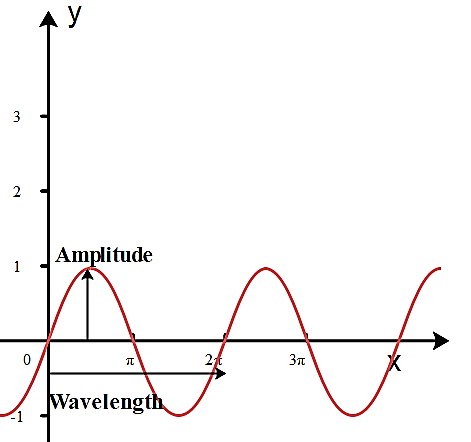
Note:
A periodic function such as $\sin x$ or $\cos x$ oscillates back and forth between the maximum and minimum value of it. The minimum value of the function will be zero and the maximum value is $2\pi$ for one complete oscillation except for the periodic function $\tan x$ which is from 0 to $\pi$.A sine wave can be otherwise called a sinusoidal wave. This is defined as a mathematical curve that explains a smooth periodic oscillation. A sine wave will be a continuous wave. It has been named after the function sine, of which it is the graph. It is happening sometimes in both pure and applied mathematics, as well as engineering, physics signal processing and many other fields.