Question

How do you find the amplitude and period of $y = \dfrac{1}{2}\sin \theta ?$

Answer 1

Amplitude is the highest value of a function in its one complete cycle or one complete period.
Period is the smallest length that repeats itself in a repeating or periodic function. And since, all the trigonometric functions are periodic, hence $\sin$function is also a periodic function.

Complete step by step answer:
As we already know that the amplitude of function means the highest possible value of that function. So do you know what’s the highest value of a $\sin$ function?
Let us find out the highest value of a $\sin$function with the help of its graph.

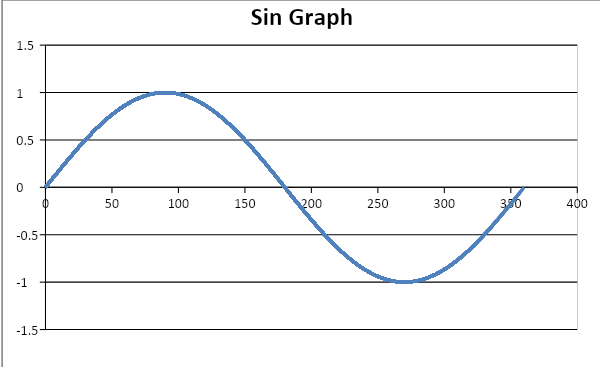
Now, from the graph we know the highest value of a $\sin$ function is $1$, therefore required amplitude will be the highest value of $y$ in the equation
$y = \dfrac{1}{2}\sin \theta$
Here in the equation $\dfrac{1}{2}$ is constant, so the only variable which can affect the value of $y$ is $\sin \theta$
And from the graph, we know the highest value of $\sin \theta$, which is equal to $1$
So, substituting the highest value of $\sin \theta$ which is $1$ in the above equation we get,
$\Rightarrow y = \dfrac{1}{2}\sin \theta \\\ \Rightarrow y = \dfrac{1}{2} \times 1 \\\ \Rightarrow y = \dfrac{1}{2} \\\$
Therefore the amplitude of the function $y = \dfrac{1}{2}\sin \theta$ is $\dfrac{1}{2}$
Now, coming to the period as from the above graph we get to know that the period of $\sin$function is $2\pi$ or ${360^ \circ }$ (in degrees)
But we have to find the period of $\dfrac{1}{2}\sin \theta$,
Here, we can see that $\dfrac{1}{2}$ is multiplied to the outcomes or $y -$ values of the function.
Therefore it will not affect the period until and unless the angle part which is $\theta$ being multiplied or divided by it.

Therefore, the required period is $2\pi$ and amplitude is $\dfrac{1}{2}$

Note: When tackling this type of more questions then here is the general formula to find amplitude and period of a sine function. If $\sin$function is written as $a\sin b\theta$, then the amplitude and period is given by Amplitude $= a$ and period $= \dfrac{{2\pi }}{b}$