Question

How do you find the amplitude and period of a function $y=\sin \left( 4x \right)$ ?

Answer 1

We are given a function as $y=\sin 4x$ , we have to find the amplitude and period, to do so we will learn about periodic function, then we learn about amplitude and the period. We will learn how the sin function is defined general then we learn from its general equation what are amplitude, what are period, vertical shift and other things we will use $y=a\sin \left( b\left( x+c \right) \right)+d$ .

Complete step by step solution:
We are given an equation of a function as $y=\sin \left( 4x \right)$ .
We are asked to find the amplitude and period of this function, before we work on that we will learn what type of sin function.
We know sin is a periodic function, periodic functions are those functions whose value keeps on repeating after a fixed amount of time that fixed time is denoted or defined as period Amplitude of function in the distance between the centre line of the function and the top or bottom of the function.
Period is also defined as the time required completing one full cycle.
We have to find the amplitude and period of $\sin \left( 4x \right)$ .
So, we will start our solution by understanding general sine function.
Generally sin function is given as –
$y=A\sin \left( B\left( x \right)+C \right)+D$
Where ‘A’ denotes the Amplitude.
$\dfrac{2\pi }{B}$ denotes the period.
C denotes the horizontal shift (phase shift) and
D denotes the vertical shift.
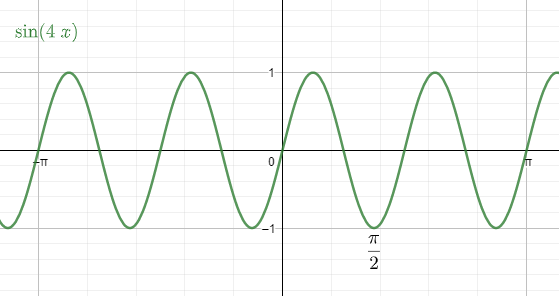
Now in our equation $y=\sin \left( 4x \right)$ , we can see that we have $A=1,B=4x,C=0\text{ and }D=0$ so, as A denotes the Amplitude and our $A=1$ , hence it mean amplitude of $y=\sin \left( 4x \right)$ is 1.
As we get that $B=4$ .
So, since period of sine function is defined as –
$\dfrac{2\pi }{B}=\text{period}$ .
So, using $B=4$ so we get –
$\begin{aligned} & \Rightarrow \text{Period}=\dfrac{2\pi }{4} \\\ & =\dfrac{\pi }{2} \\\ \end{aligned}$
So, the period of $\sin \left( 4x \right)$ is $\dfrac{\pi }{2}$ , here after each $\dfrac{\pi }{2}$ at time, it start a new cycle.

Note: When we find the period from graph, we look how much time its take to complete one cycle, that time directly become the period for the amplitude using graph we just use the identify $\text{Amplitude}=\dfrac{\text{highest point }-\text{ lowest point}}{2}$ highest and lowest point of the graph where any graph is reach.
For another point, that is horizontal or vertical we use identify to find these values using graphs.