Question

How do you find the absolute value of a number?

Answer 1

We explain the term absolute value of a number. How the absolute value always remains positive. We expand the function and break it into two parts. Then we verify the result with an example.

Complete step by step answer:
Absolute value means the distance of the number from 0. The number can be both positive and negative but the distance of that number will always be positive. Distance can never be negative.
In mathematical notation we express it with modulus value. Let a number be x whose sign is not mentioned. The absolute value of that number will be $\left| x \right|$. We can say $\left| x \right|\ge 0$.
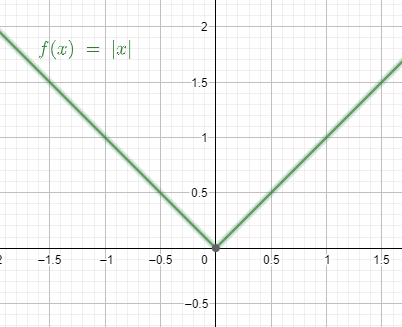
We can express the function $f\left( x \right)=\left| x \right|$ as f\left( x \right)=\left\\{ \begin{matrix} x\left( x\ge 0 \right) \\\ -x\left( x<0 \right) \\\ \end{matrix} \right..
If the value of the number is 0 or greater than 0 which means positive then we take the value of that number as its absolute value and If the value of the number is less than 0 which means negative then we take the negative value of that number as its absolute value.
Let us explain the theorem with an example where we take the value of x as $x=7$. As $x>0$, the absolute value $f\left( 7 \right)=\left| 7 \right|=7$ is the number itself. Now we take $x=-4$. As $x<0$, the absolute value $f\left( -4 \right)=\left| -4 \right|=-\left( -4 \right)=4$ is the negative of the number itself.

Note: The only time the absolute value becomes 0 is when the number itself is 0. For any other number the absolute value is greater than 0. Therefore, we can say $\left| x \right|>0$ when $x\ne 0$. The graph of the function is