Question

How do you find the absolute value equation from a graph?

Answer 1

Absolute value equations are equations where the variable is within an absolute value operator, like $\left| x-3 \right|=5$. The absolute value of a number depends on the number's sign: if it is positive, it is equal to the number: $\left| 5 \right|=5$. If the number is negative, then the absolute value is its opposite: $\left| -5 \right|=5$. So, when we are dealing with a variable, we need to consider both the cases.

Complete step by step answer:
The general form of an absolute value equation is $y=a\left| x-h \right|+k$. The variable tells us how far the graph stretches vertically, and whether the graph opens up or down. The variables and tell us how far the graph shifts horizontally and vertically.
As per the given question, we need to find the absolute value equation from graph. The graph of an absolute value equation will be shaped like V or an upside down V.
Let the vertex be $\left( h,k \right)$. The vertex is the point where the two straight lines meet, to find the vertex we look at a graph where two straight lines meet and note that point as the vertex.
The two straight lines are present such that one is on the left side of the vertex and the other is present on the right side of the vertex.
To the right side of the vertex, let the slope of the line be a. then the slope of the line left to the vertex is -a. when we find the vertex, then we need to find another point on the graph.
If we find the another point on the graph to right side of the vertex then the slope will be a which is equal to
Let the point be $\left( {{x}_{2}},{{y}_{2}} \right)$ and the vertex is $\left( h,k \right)$
$a=\dfrac{{{y}_{2}}-k}{{{x}_{2}}-h}$
In this way we can find the value of a. now on substituting the value of a and vertex $\left( h,k \right)$. We can get the absolute value equation from the graph.

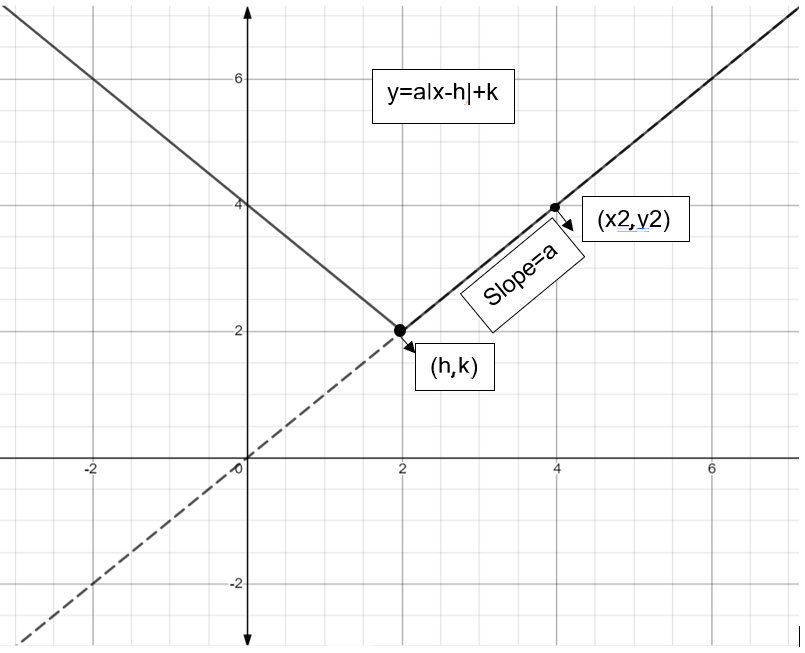
If we find the other point to the left side of the graph then the slope will be equal to, -a.

Therefore, the equation will be $y=a\left| x-h \right|+k$.

Note: While solving these types of problems, we need to have enough knowledge over absolute value equations and their functions. While finding vertex check whether it is in the form $y=a\left| x-h \right|+k$ or $y=a\left| x-h \right|-k$. Because the vertex changes for $y=a\left| x-h \right|-k$ that is $\left( h,-k \right)$. We should avoid calculation mistakes to get the correct results.