Solveeit Logo
Login

Question

Question: How do you find slope and intercepts to graph \(9x-5y=4\)?...

How do you find slope and intercepts to graph 9x−5y=49x-5y=4?

Explanation

Solution

In the above question, we have been given an equation of a straight line, since it is linear in both x and y. The slope is defined as the derivative of y with respect to x. Therefore, on differentiating the given equation with respect to x, we can solve the resulting equation for dydx\dfrac{dy}{dx} to get the value of the slope. And the intercept is the point on which the graph of a function intersects the y-axis. Therefore, we will put x=0x=0 in the given equation and on solving the resulting equation for y, we will obtain the value of the intercept.

Complete step-by-step answer:
The equation given in the above question is
⇒9x−5y=4\Rightarrow 9x-5y=4
Since the above equation is linear in both x and y, it is the equation of a straight line. Now, we know that the slope is equal to the derivative of y with respect to x. Therefore, we differentiate the above equation with respect to x to get
⇒d(9x−5y)dx=d(4)dx ⇒9−5dydx=0 \begin{aligned} & \Rightarrow \dfrac{d\left( 9x-5y \right)}{dx}=\dfrac{d\left( 4 \right)}{dx} \\\ & \Rightarrow 9-5\dfrac{dy}{dx}=0 \\\ \end{aligned}
Subtracting 99 from both the sides, we get
⇒9−5dydx−9=0−9 ⇒−5dydx=−9 \begin{aligned} & \Rightarrow 9-5\dfrac{dy}{dx}-9=0-9 \\\ & \Rightarrow -5\dfrac{dy}{dx}=-9 \\\ \end{aligned}
Dividing both the sides by −5-5, we get
⇒dydx=−9−5 ⇒dydx=95 \begin{aligned} & \Rightarrow \dfrac{dy}{dx}=\dfrac{-9}{-5} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{9}{5} \\\ \end{aligned}
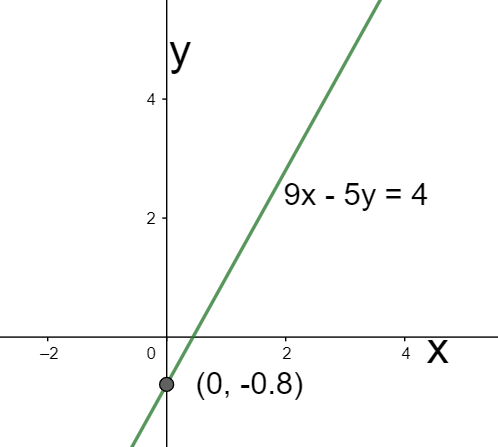
Hence, the slope is equal to 95\dfrac{9}{5}.
Now, we know that the intercept is the point where the graph intersects the y-axis. Since the equation o y-axis is x=0x=0, we substitute it in the given equation to get
⇒9(0)−5y=4 ⇒−5y=4 ⇒y=−45 \begin{aligned} & \Rightarrow 9\left( 0 \right)-5y=4 \\\ & \Rightarrow -5y=4 \\\ & \Rightarrow y=-\dfrac{4}{5} \\\ \end{aligned}
Hence, the intercept is equal to −45-\dfrac{4}{5}. In decimal form, we can write it as -0.8.
We can observe these in the below graph.

Note: We can also easily determine the slope and intercept of the given equation using the by writing it in the slope-intercept form, which is given as y=mx+cy=mx+c. For this, we need to separate y on the LHS such that its coefficient is equal to one. Then the coefficient of x will be equal to the sloep and the constant term will be equal to the intercept.