Solveeit Logo
Login

Question

Question: How do you find sine, cosine or tangent of \( {90^ \circ } \) or \( {180^ \circ } \) using the unit ...

How do you find sine, cosine or tangent of 90∘{90^ \circ } or 180∘{180^ \circ } using the unit circle ?

Explanation

Solution

Hint : In the given problem, we are required to find the sine, cosine or tangent of a given angle using some simple and basic trigonometric ideas and methods. Such questions require basic knowledge of compound angle formulae and their applications in this type of questions. Unit circle is a circle with a radius of one unit drawn on a graph paper with its centre at origin.

Complete step by step solution:
Consider a unit circle (a circle of radius of 1 unit centered at origin).
We need to find out the values of sine, cosine and tangent using the unit circle for angles 90∘{90^ \circ } or 180∘{180^ \circ } .
We know that sin⁡θ=AltitudeHypotenuse\sin \theta = \dfrac{{{\text{Altitude}}}}{{{\text{Hypotenuse}}}} , tan⁡θ=AltitudeBase\tan \theta = \dfrac{{{\text{Altitude}}}}{{{\text{Base}}}} and cos⁡θ=BaseHypotenuse\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} .

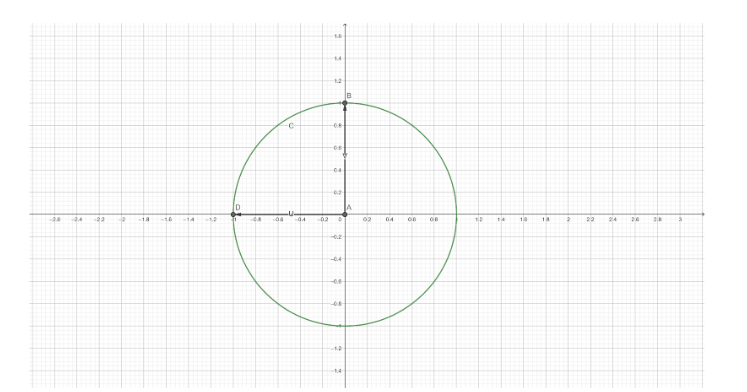
Now, observing the figure, we can infer a lot of things and parameters.
For 90∘{90^ \circ } ,
Altitude =1= 1
Base =0= 0
Hypotenuse =1= 1
So, sin⁡90∘=AltitudeHypotenuse=1\sin {90^ \circ } = \dfrac{{{\text{Altitude}}}}{{{\text{Hypotenuse}}}} = 1
cos⁡90∘=BaseHypotenuse=0\cos {90^ \circ } = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = 0
tan⁡90∘=AltitudeBase=10 = Not defined\tan {90^ \circ } = \dfrac{{{\text{Altitude}}}}{{{\text{Base}}}} = \dfrac{1}{0}{\text{ = Not defined}}

For 180∘{180^ \circ } ,
Altitude =0= 0
Base =1= 1
Hypotenuse =1= 1
So, sin⁡90∘=AltitudeHypotenuse=0\sin {90^ \circ } = \dfrac{{{\text{Altitude}}}}{{{\text{Hypotenuse}}}} = 0
cos⁡90∘=BaseHypotenuse=1\cos {90^ \circ } = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = 1
tan⁡90∘=AltitudeBase=0\tan {90^ \circ } = \dfrac{{{\text{Altitude}}}}{{{\text{Base}}}} = 0
Hence, the values of sine, cosine and tangent for the angles 90∘{90^ \circ } or 180∘{180^ \circ } using the unit circle can be calculated as done above in the solution.

Note : The method discussed in the question to find the value of sine, cosine, tangent or any other trigonometric function is fundamental and basic. The answers for the values of sine, cosine and tangent ratios for the given values of angles can also be verified using the table of trigonometric value tables for special angles.