Question

How do you find its vertex, axis of symmetry, y-intercept and x-intercept for $f(x)=-3{{x}^{2}}+3x-2$?

Answer 1

We are given with a quadratic equation using which the above mentioned properties have to be found. Since the equation is of the form $y=-{{x}^{2}}$, so it is a parabola open towards the negative y – axis. And we will find the axis of symmetry and x-vertex using the formula $x=\dfrac{-b}{2a}$ and for y –vertex, substitute the value x – vertex in the given equation. Y-intercept is found by keeping $x=0$ and vice – versa.

Complete step by step solution:
According to the given question, we have been given a quadratic equation, whose mentioned properties we have to find.
We have the given expression as
$f(x)=-3{{x}^{2}}+3x-2$----(1)
Here, $a=-3,b=3,c=-2$
We will begin with vertex.
Vertex of a parabola can simply be said as the intersection point between the line of symmetry and the parabola.
X – coordinate of vertex $=\dfrac{-b}{2a}$
On substituting, we get it as,
$\Rightarrow \dfrac{-3}{2(-3)}$
$\Rightarrow \dfrac{1}{2}$
So, we have the x-coordinate of the vertex. For y- coordinate, we will substitute the value of x in the equation (1), we get,
$y=-3{{x}^{2}}+3x-2$
$\Rightarrow y=-3{{\left( \dfrac{1}{2} \right)}^{2}}+3\left( \dfrac{1}{2} \right)-2$
$\Rightarrow y=-3\left( \dfrac{1}{4} \right)+3\left( \dfrac{1}{2} \right)-2$
$\Rightarrow y=\dfrac{-3}{4}+\dfrac{3}{2}-2$
$LCM(4,2)=4$
$\Rightarrow y=\dfrac{-3}{4}+\dfrac{3}{2}\times \dfrac{2}{2}-2\times \dfrac{4}{4}$
On solving further, we get,
$\Rightarrow y=\dfrac{-3}{4}+\dfrac{6}{4}-\dfrac{8}{4}$
$\Rightarrow y=\dfrac{-3+6-8}{4}$
$\Rightarrow y=\dfrac{-5}{4}$
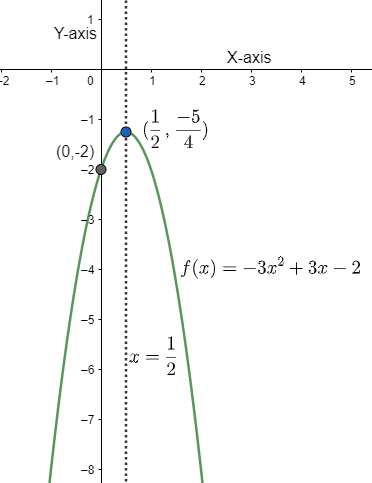
So, the vertex of the parabola is $\left( \dfrac{1}{2},\dfrac{-5}{4} \right)$.
As we have stated that vertex is the intersection of the line of symmetry and the parabola. And the equation of parabola we have is open towards the negative y-axis. This means that the x – coordinate of the vertex is the same as the equation of line of symmetry passing through the vertex.
Therefore, the line of symmetry is $x=\dfrac{1}{2}$.
Now, we will find the y – intercept. We know that, y- intercept refers to the point when the given equation intersects with y- axis, so at that point we have $x=0$. Therefore, to find the y-intercept we will put $x=0$ in the given quadratic equation.
We have,
$y=-3{{x}^{2}}+3x-2$
Substituting $x=0$, we get,
$\Rightarrow y=-3{{(0)}^{2}}+3(0)-2$
$\Rightarrow y=-2$
Therefore, the point of y-intercept is $(0,-2)$.
Now, we have to find the x-intercept. It is a point that the equation makes with the x-axis. At that point $y=0$. So, to find the x-intercept, we will put $y=0$ in the given quadratic equation. We have,
$-3{{x}^{2}}+3x-2=0$
Since we cannot factor it, we will use discriminant, we get,
$D={{b}^{2}}-4ac$
$D={{(3)}^{2}}-4(-3)(-2)$
$D=9-24$
$D=-15<0$
Since, the value is less than zero, we will not have any real roots for the given quadratic equation. Therefore, the equation does not have a x – intercept.
The graph of the given equation is as follows:

Note:
The line of symmetry and vertex are related. In the above question, we had the parabola opening toward the negative y-axis, so the line of symmetry was similar to the x-coordinate of the vertex. But if we had the parabola opening towards the x-axis, then the line of symmetry would be the y-coordinate of the vertex.
Also, since the above question involves multiple properties to be found. Therefore, it should be done neatly and in an organized manner.