Question

How do you find intercepts, extrema, points of inflections, asymptotes and graph $y={{x}^{5}}-5x$?

Answer 1

We are given with an expression whose, above mentioned properties we have to find. To find the x-intercept, we will put $y=0$ in the given expression and for y-intercept, we will put $x=0$ and solve it. We can find the points of extrema (minimum or maximum points) by taking the first derivative of the given expression and then equating it to 0. For points of inflection, we have to use the second derivative. The point of inflection has the function increasing in one direction and decreasing in the other directions. Asymptote can be found by observing the graph of the equation as it is the line that approaches a value but never actually meets.

Complete step by step solution:
According to the given question, we have a polynomial whose, above mentioned properties are to be found. The given equation we have is,
$y={{x}^{5}}-5x$----(1)
We will start by finding the x-intercept. We know that, x-intercept is the intersection of the graph of the given function and the x-axis. The y-coordinate at this point is 0. So, we will put $y=0$ to find the x-intercept. We have,
$y={{x}^{5}}-5x$
$\Rightarrow {{x}^{5}}-5x=0$
$\Rightarrow x({{x}^{4}}-5)=0$
So, we have either $x=0$ or ${{x}^{4}}-5=0$. We get,
$\Rightarrow {{x}^{4}}=5$
$\Rightarrow x=\pm \sqrt[4]{5}$
We have the points of x-intercept as $(0,0),(\sqrt[4]{5},0),(-\sqrt[4]{5},0)$.
Now, we have to find the y-intercept, for that we will put $x=0$ in the given polynomial equation and we get,
$y={{x}^{5}}-5x$
$\Rightarrow y=0$
Therefore, the point of y-intercept is $(0,0)$.
Now, we have to find the extrema. Extrema refers to the maximum or the minimum value that a function can have. We will find the extrema of the given equation by using First Derivative. We have,
$y={{x}^{5}}-5x$
Differentiating on both sides we have,
$\Rightarrow y'=\dfrac{d}{dx}({{x}^{5}}-5x)$
$\Rightarrow y'=\dfrac{d}{dx}({{x}^{5}})-\dfrac{d}{dx}(5x)$
$\Rightarrow y'=5{{x}^{4}}-5$----(2)
Taking 5 common from the above expression, and factorizing the equation, we get,
$\Rightarrow y'=5({{x}^{4}}-1)$
We will use, ${{a}^{2}}-{{b}^{2}}=(a+b)(a-b)$, we get
$\Rightarrow y'=5({{x}^{2}}+1)({{x}^{2}}-1)$
$\Rightarrow y'=5({{x}^{2}}+1)(x-1)(x+1)$
Now, we will equate it to 0, we get,
$5({{x}^{2}}+1)(x-1)(x+1)=0$
$x=1$ and $x=-1$
That is, for these values of x we have the equation to have 0.
So, these can be maxima or minima points, for that we will use the second derivative test,
Differentiating the equation (2) further, we get,
$y'=5{{x}^{4}}-5$
$\Rightarrow y''=20{{x}^{3}}$------(3)
Using $x=-1$ in equation (3),
We have,
$y''=20{{x}^{3}}$
$\Rightarrow y''=20{{(-1)}^{3}}=-20$
That is, $x=-1$ will have a maxima.
Substituting this value in the equation (1), we will get the value of y,
$y={{x}^{5}}-5x$
$\Rightarrow y={{(-1)}^{5}}-5(-1)=4$
so the point is $(-1,4)$
And for $x=1$,
$\Rightarrow y''=20{{(1)}^{3}}=20$
So, we will have a minima for $x=1$.
Similarly, substituting this value in the equation (1), we will get the point as $(1,-4)$.
From the given points that we have, we draw the graph of the given equation, we get,

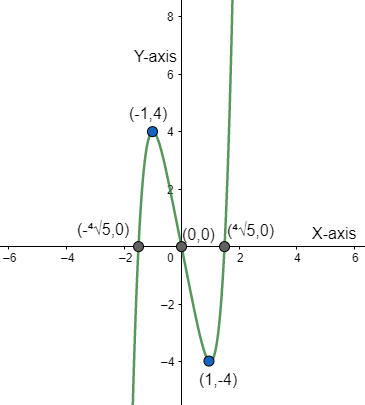
So, we do not have absolute maxima or minima as from the above graph, we can see that the graph extends indefinitely in both the directions. But we do have relative maxima and minima, which are,
Relative maxima is $(-1,4)$
Relative minima is $(1,-4)$
Point of inflection refers to the points where the function increases in one direction and decreases in all other directions. We can find this by equating the second derivative of the given polynomial to 0. That is, we will equate equation (3) to 0, we get,
$y''=20{{x}^{3}}=0$
$\Rightarrow 20{{x}^{3}}=0$
$\Rightarrow x=0$
We get the inflection point as $x=0$, we will now check if the given function changes sign across $x=0$.
As we already saw above that, at $x=-1$, the function was increasing and at $x=1$ the function was decreasing. Therefore, $x=0$ is an inflection coordinate.
Putting this value of $x=0$ in equation (1), we get, $y=0$.
Therefore, the inflection point is $(0,0)$.
Asymptotes can be referred to a line which is not the part of the function and the graph of that function approaches it, but never meets it. Rational functions have asymptotes.
Therefore, the given polynomial equation has no asymptotes.

Note:
The given equation does not have an asymptote as asymptotes are usually found in a rational fraction, where the polynomial in the numerator and the denominator can have the similar degree or different. There are usually two types of asymptotes: horizontal asymptote and vertical asymptote. The calculation of each of the properties asked in the question for the given polynomial equation should be done in separate stages and in separate steps, so as to avoid complications while solving the question.