Question

How do you find horizontal asymptotes for $f\left( x \right)={{\tan }^{-1}}\left( x \right)$ ?

Answer 1

To solve these types of problems efficiently, one has to have a fair knowledge of graph theory and asymptotes of a graph. Knowledge of inverse functions is also necessary. Asymptotes are defined as the lines, which meet a curve at infinity. In these types of questions, we first plot the graph for the original trigonometric function, here which is $\tan \left( x \right)$ and then take its reflection about the line $y=x$ to draw the graph of its inverse function. This is pretty much the straight forward rule to draw the graph for inverse functions.

Complete step by step answer:
Now starting off with the problem, we know that, when we try to calculate the value of $\tan \left( \dfrac{\pi }{2} \right)$ or $\tan \left( -\dfrac{\pi }{2} \right)$ or $\tan \left( \dfrac{n\pi }{2} \right)$ (where ‘n’ is any integer, positive or negative), it comes out to be undefined, which means that the vertical line $x=n\dfrac{\pi }{2}$ is an asymptote of the curve $\tan \left( x \right)$ . Now since the reflection of the curve $y=\tan \left( x \right)$ about the line $y=x$ gives the graph for the inverse curve that is $y={{\tan }^{-1}}\left( x \right)$, reflection of $x=n\dfrac{\pi }{2}$ about the line $y=x$ will also give the required equation of the horizontal asymptote. Thus we can safely say that $y={{\tan }^{-1}}\left( \infty \right)$ and $y={{\tan }^{-1}}\left( -\infty \right)$ will be the equations of the horizontal asymptotes of the equation $y={{\tan }^{-1}}\left( x \right)$ . We can further write that $y={{\tan }^{-1}}\left( \tan \left( \dfrac{n\pi }{2} \right) \right)$ is the general equation for the asymptote. Thus,
$y=\dfrac{n\pi }{2}$ , is the equation of the horizontal asymptote, where ‘n’ is any integer, positive or negative.

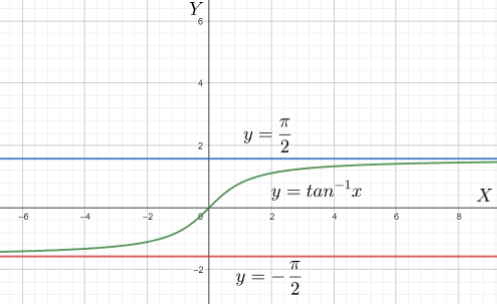
Note: We have to be very careful regarding the domain and range of the problem. In this question since no domain and range is given, the method done here is a more generalized one. After plotting the graph, we need to closely analyse for the lines which may meet the graph at infinity.