Solveeit Logo
Login

Question

Question: How do you find \[\cos \] if \[\sin = \left( {\dfrac{5}{{13}}} \right)\] ?...

How do you find cos⁡\cos if sin⁡=(513)\sin = \left( {\dfrac{5}{{13}}} \right) ?

Explanation

Solution

Hint : We are given the value of sine function and asked to find the value of cosine. To know the value of cosine we will need an equation to convert sine to cosine. For this you will need to recall a trigonometric identity of sine and cosine. Use this trigonometric identity to find the value of cosine.

Complete step-by-step answer :

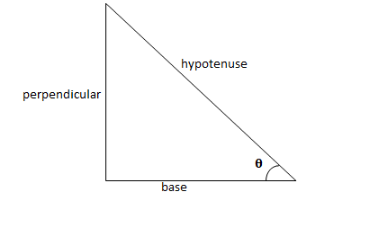
In case of a right angled triangle, we can write hypotenuse, base and perpendicular in terms of sine and cosine function as,
sin⁡θ=perpendicularhypotenuse\sin \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} and cos⁡θ=basehypotenuse\cos \theta = \dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}}
Given, sin⁡=(513)\sin = \left( {\dfrac{5}{{13}}} \right)
We are asked to find the value of cosine function.
To find cosine we need an equation to convert sine function to cosine function.
From trigonometric identities, we have an equation,
sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1 (i)
Here, sin⁡θ=(513)\sin \theta = \left( {\dfrac{5}{{13}}} \right)
Putting this value in equation (i) we get,
(513)2+cos⁡2θ=1{\left( {\dfrac{5}{{13}}} \right)^2} + {\cos ^2}\theta = 1
⇒cos⁡2θ=1−(513)2\Rightarrow {\cos ^2}\theta = 1 - {\left( {\dfrac{5}{{13}}} \right)^2}
⇒cos⁡2θ=1−25169\Rightarrow {\cos ^2}\theta = 1 - \dfrac{{25}}{{169}}
⇒cos⁡2θ=144169\Rightarrow {\cos ^2}\theta = \dfrac{{144}}{{169}}
⇒cos⁡θ=±144169\Rightarrow \cos \theta = \pm \sqrt {\dfrac{{144}}{{169}}}
⇒cos⁡θ=±1213\Rightarrow \cos \theta = \pm \dfrac{{12}}{{13}}
Therefore, the value of cosine is ±1213 \pm \dfrac{{12}}{{13}} .
So, the correct answer is “ ±1213 \pm \dfrac{{12}}{{13}} ”.

Note : There are three main functions in trigonometry, these are sine, cosine and tangent. There are three other trigonometric functions which can be written in terms of the main functions, these are cosecant which is inverse of sine, secant which is inverse of cosine and cotangent which is inverse of tangent. Also, while solving questions related to trigonometry, you should always remember the basic trigonometric identities. The trigonometric identity sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1 is also known as Pythagorean identity.