Question

How do you find an equation of the line that contains the following pair of points $\left( { - 4, - 5} \right)$ and $\left( { - 8, - 10} \right)$ ?

Answer 1

In this problem we have to find the equation of a line with two points. The equation of a line passing through two points $\left( {{x_1},{\text{ }}{y_1}} \right)$ and $\left( {{x_2},{\text{ }}{y_2}} \right)$ is given by $\dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{x - {x_1}}}{{{x_2} - {x_1}}}$ . Hence, we will use this two-point form of the equation to get the required equation of the line. After that we will rearrange the equation in the standard form i.e., $ax + by + c = 0$ . and hence we will get the required equation of the line.

Complete step by step answer:
We have given two points on the line.
Let $\left( { - 4, - 5} \right)$ be $\left( {{x_1},{\text{ }}{y_1}} \right)$ and $\left( { - 8, - 10} \right)$ be $\left( {{x_2},{\text{ }}{y_2}} \right)$
We have to find the equation of the line passing through these two points.
Now we know that according to the two-point form, the equation of a line passing through two points $\left( {{x_1},{\text{ }}{y_1}} \right)$ and $\left( {{x_2},{\text{ }}{y_2}} \right)$ is given by
$\dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{x - {x_1}}}{{{x_2} - {x_1}}}$
Here, ${x_1} = - 4,{\text{ }}{x_2} = - 8,{\text{ }}{y_1} = - 5,{\text{ }}{y_2} = - 10$
So, on substituting the values, we get
$\Rightarrow \dfrac{{y - \left( { - 5} \right)}}{{\left( { - 10} \right) - \left( { - 5} \right)}} = \dfrac{{x - \left( { - 4} \right)}}{{\left( { - 8} \right) - \left( { - 4} \right)}}$
On simplification, we get
$\Rightarrow \dfrac{{y + 5}}{{ - 5}} = \dfrac{{x + 4}}{{ - 4}}$
Now cross multiplying the equation, we get
$\Rightarrow - 4\left( {y + 5} \right) = - 5\left( {x + 4} \right)$
On multiplying, we get
$\Rightarrow - 4y - 20 = - 5x - 20$
$\Rightarrow - 4y = - 5x$
Now rearranging the equation in the standard form i.e., $ax + by + c = 0$ we get
$- 5x + 4y + 0 = 0$
Taking $- 1$ common, we get
$5x - 4y = 0$
Hence the required equation passing through $\left( { - 4, - 5} \right)$ and $\left( { - 8, - 10} \right)$ is $5x - 4y = 0$
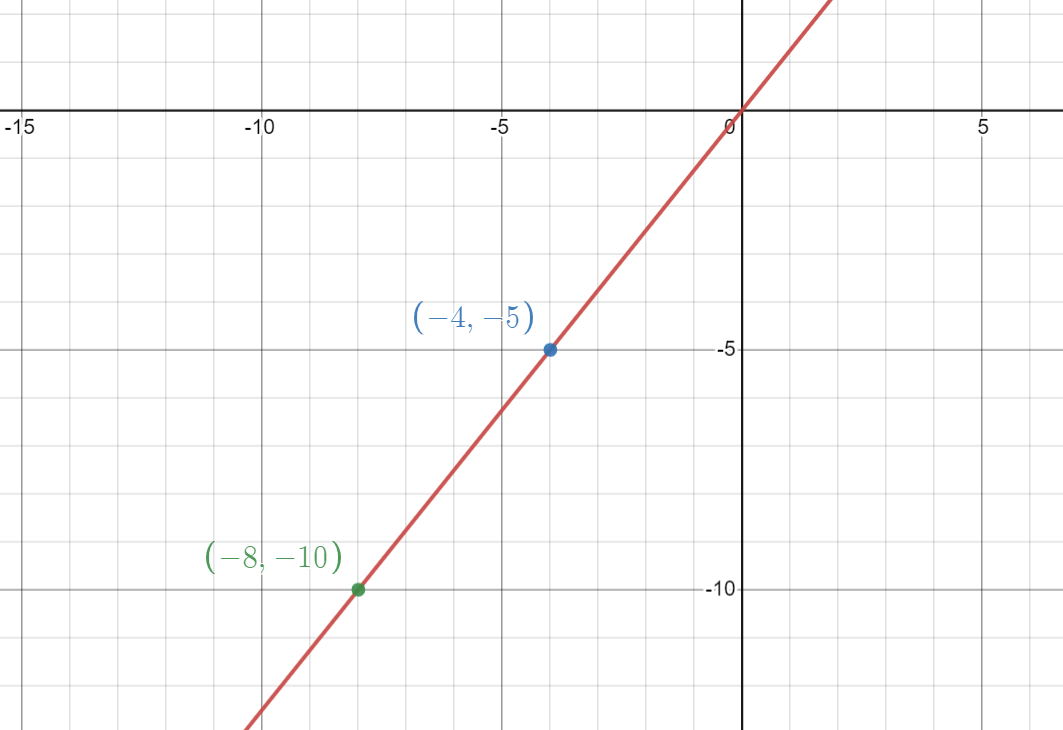
We can see the same information in the below graph:

Note:
This question can also be solved using slope intercept form.
We know that the slope intercept form of the line is given by
$y = mx + c{\text{ }} - - - \left( i \right)$
where $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ is the slope and $c$ is the y-intercept.
Now we have two points,
Let $\left( {{x_1},{\text{ }}{y_1}} \right) = \left( { - 4, - 5} \right)$ and $\left( {{x_2},{\text{ }}{y_2}} \right) = \left( { - 8, - 10} \right)$
Therefore, on substituting the values
Slope, $m = \dfrac{{\left( { - 10} \right) - \left( { - 5} \right)}}{{\left( { - 8} \right) - \left( { - 4} \right)}}$
$\Rightarrow m = \dfrac{{ - 10 + 5}}{{ - 8 + 4}}$
$\Rightarrow m = \dfrac{5}{4}$
On substituting in equation $\left( i \right)$ we get
$y = \dfrac{5}{4}x + c$
Now substitute the value of $x$ and $y$ from any of the two points to get the y-intercept.
Let’s take the point $\left( { - 4, - 5} \right)$
Therefore, we have
$- 5 = \dfrac{5}{4}\left( { - 4} \right) + c$
$\Rightarrow c = 0$
Thus, the y-intercept is $0$ and the slope is $\dfrac{5}{4}$
Therefore, slope intercept form of the line will be
$y = \dfrac{5}{4}x$
On rearranging in the standard form, we get
$5x - 4y = 0$
Hence, we get the required equation of the line passing through $\left( { - 4, - 5} \right)$ and $\left( { - 8, - 10} \right)$