Question

How do you find an equation of the line containing the given pair of points $\left( -7,-4 \right)$ and $\left( -2,-6 \right)$?

Answer 1

We first try to express the formula or equation for the line whose two points’ coordinates are given. The points are contained in the line. We express the equation based on two arbitrary points and then put the coordinates of the given points.

Complete step by step solution:
We need to find the equation of the line containing the given pair of points $\left( -7,-4 \right)$ and $\left( -2,-6 \right)$.
We take two arbitrary points. They are $\left( a,b \right);\left( c,d \right)$.
Then the equation of the line containing the points is $\dfrac{y-b}{b-d}=\dfrac{x-a}{a-c}$.
Now, we find the equation of the line with points $\left( -7,-4 \right)$ and $\left( -2,-6 \right)$.
The replacement will be $\left( a,b \right)\equiv \left( -7,-4 \right);\left( c,d \right)\equiv \left( -2,-6 \right)$ for the theorem $\dfrac{y-b}{b-d}=\dfrac{x-a}{a-c}$.
The equation of the line will be $\dfrac{y-\left( -4 \right)}{\left( -4 \right)-\left( -6 \right)}=\dfrac{x- \left( -7 \right)}{\left( -7 \right)-\left( -2 \right)}$.
Simplifying the equation, we get
$\begin{aligned} & \dfrac{y+4}{-4+6}=\dfrac{x+7}{-7+2} \\\ & \Rightarrow -5\left( y+4 \right)=2\left( x+7 \right) \\\ & \Rightarrow 2x+5y+34=0 \\\ \end{aligned}$
The required equation of the line containing the given pair of points $\left( -7,-4 \right)$ and $\left( -2,-6 \right)$ is $2x+5y+34=0$.

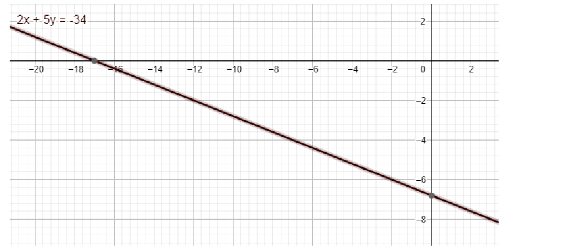
Note: We are taking the general equation of line to understand the slope and the intercept form of the line $2x+5y=-34$.
The given equation $2x+5y=-34$ is of the form $ax+by=c$. Here a, b, c are the constants.
We convert the form to $y=mx+k$. m is the slope of the line.
So, converting the equation we get
$\begin{aligned} & 2x+5y=-34 \\\ & \Rightarrow y=-\dfrac{2}{5}x-\dfrac{34}{5} \\\ \end{aligned}$
This gives that the slope of the line $2x+5y=-34$ is $-\dfrac{2}{5}$.