Question

How do you find an equation of hyperbola with given endpoints of the transverse axis: $y = \dfrac{3}{{10}}x$ Asymptote: $y = \dfrac{3}{{10}}x$ ?

Answer 1

Hint : We need to find the equation of hyperbola with the given points foci, $F(0, \pm a)$ of the transverse axis and asymptote equation of the transverse axis.
The equation of asymptote is $y = \dfrac{a}{b}x$ ………………. $(A)$
The equation of hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ ………………… $(B)$
To plot a graph by the given points mentioned below

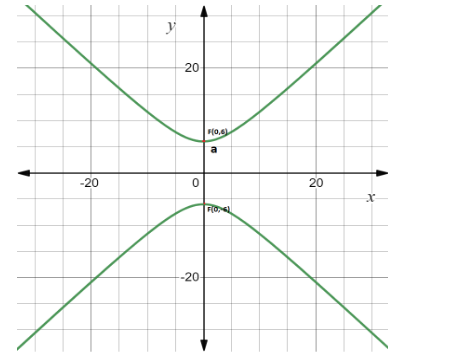
** Complete step-by-step answer** :
Given,
Focus, $F = (0, \pm 6)$
Where, $a = 6$ .
The given asymptote equation, we have
$y = \dfrac{3}{{10}}x$ …………… $(1)$
By substitute the equation $(A)$ in $(1)$ , we get
$\dfrac{a}{b}x = \dfrac{3}{{10}}x$
By remove $x$ on both sides, we get
$\dfrac{a}{b} = \dfrac{3}{{10}}$
By substitute the value, $a = 6$
$\dfrac{6}{b} = \dfrac{3}{{10}}$
By simplify the above to find the value,

$$6 \times 10 = 3b \\\ b = \dfrac{{60}}{3} = 20 \;$$

Now, we get
$b = 20$
To find the equation of hyperbola by substitute the value to the formula
We know that,
The equation of hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$
Here, we have the value $a = 6,b = 20$
To substitute the values, we get
$\dfrac{{{x^2}}}{{{6^2}}} - \dfrac{{{y^2}}}{{{{20}^2}}} = 1$
By simplify the square of denominator, we get
$\dfrac{{{x^2}}}{{36}} - \dfrac{{{y^2}}}{{400}} = 1$
Hence, the equation of hyperbola is $\dfrac{{{x^2}}}{{36}} - \dfrac{{{y^2}}}{{400}} = 1$
So, the correct answer is “$\dfrac{{{x^2}}}{{36}} - \dfrac{{{y^2}}}{{400}} = 1$ ”.

Note : We need to find the equation of hyperbola with the given focus and equation of asymptote of the transverse axis. To solve the equation of hyperbola by finding the value of $a$ and $b$ by the asymptote equation and the focus value, $F(0, \pm a)$ . We should remember the equation of parabola, hyperbola and asymptote to solve the similar problem with different values like $y = \dfrac{1}{2}x + 4$ etc.….