Question

How do you find an equation of a line containing the point $\left( 3,2 \right)$ and parallel to the line $y-2=\dfrac{2}{3}x$?

Answer 1

Change of form of the given equation $y-2=\dfrac{2}{3}x$ will give the slope of the line. We change it to the form of $y=mx+k$ to find the slope m. Then, we get into the form of its parallel line to find the equation. We put the point value of $\left( 3,2 \right)$ to find the value of the constant. We get the equation of the parallel line.

Complete step by step answer:
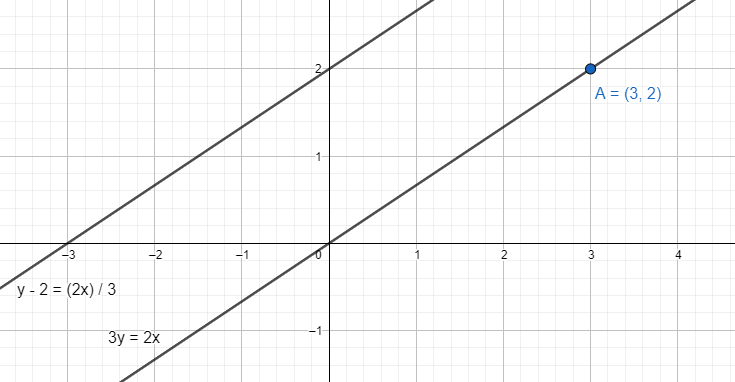
The given equation of the line $y-2=\dfrac{2}{3}x$ can be changed to $y=\dfrac{2}{3}x+2$.
The given equation $y=\dfrac{2}{3}x+2$ is of the form $y=mx+k$. m is the slope of the line.
This gives that the slope of the line $y-2=\dfrac{2}{3}x$ is $\dfrac{2}{3}$.
We know that any line parallel to the given line will be of the same slope.
This means any line parallel to $y-2=\dfrac{2}{3}x$ will have a slope of $\dfrac{2}{3}$.
We take the equation of any parallel line to $y=mx+k$ as $y=mx+c$.
Let’s assume that the parallel line to $y=\dfrac{2}{3}x+2$ as $y=\dfrac{2}{3}x+p$. Here $p$ is a constant value which we have to find out.
The parallel line goes through the point $\left( 3,2 \right)$. We place the point in the equation $y=\dfrac{2}{3}x+p$.
$\begin{aligned} & 2=\dfrac{2}{3}\times 3+p \\\ & \Rightarrow p=2-2=0 \\\ \end{aligned}$
Value of $p$ is 0.
The equation of the line is $y=\dfrac{2}{3}x$. Simplified form is $3y=2x$.

Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance and hence we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $\infty$.