Question

How do you find all the real and complex roots and use Descartes Rule of Signs to analyze the zeros of $P\left( x \right)=2{{x}^{5}}+7{{x}^{3}}+6{{x}^{2}}-2?$

Answer 1

To solve this question, we need to know Descartes rule of signs which is used to give us the number of real zeros of a given polynomial equation. The number of sign changes between the coefficients are noted which gives us the number of real zeros. After that we specify the number of remaining zeros as complex zeros. We then use it to determine the roots of the equation.

Complete step by step solution:
The given question has the polynomial $P\left( x \right)=2{{x}^{5}}+7{{x}^{3}}+6{{x}^{2}}-2.$ We now need to check for the number of sign changes in the coefficients. The 4 coefficients are +2, +7, +6 and -2. So as we can see, the signs are given as: + + + - . There is no sign change between the first and second coefficients or the second and third coefficients. Hence the number of sign changes are only 1, that is from the +6 to -2 which are the third and fourth coefficients. Hence, this equation for the function $P\left( x \right)$ has only 1 positive real zero.
Now, since we know that the equation having a degree 5 has 5 zeroes, we can say that this equation has 4 complex zeroes. This is so because firstly the number of real zeroes is 1 and complex roots always occur in pairs.
In order to find out the real zero for this equation, we plot the given function $P\left( x \right)=2{{x}^{5}}+7{{x}^{3}}+6{{x}^{2}}-2$ and observe the graph for an intersection point with the x-axis.

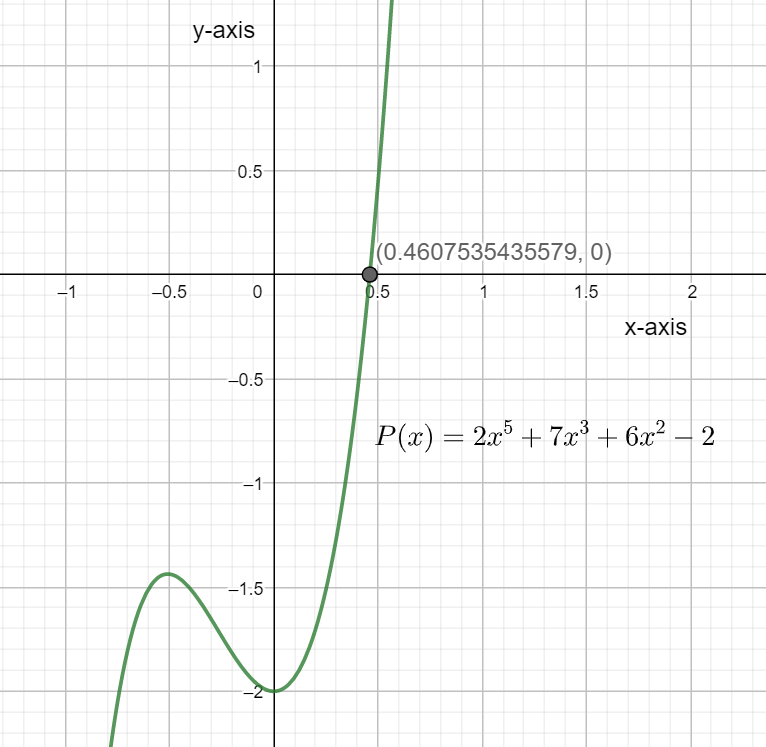
We can see that the real zero exists at the point at which x=0.4607.
We can find out the complex roots by solving the equation using any of the complex roots solving methods and we get the complex roots as:
$\Rightarrow x=-0.617273-0.377799i$
$\Rightarrow x=-0.617273+0.377799i$
$\Rightarrow x=0.386896-1.99853i$
$\Rightarrow x=0.386896+1.99853i$
Hence, we have found all the roots for the given polynomial and we have used the Descartes rule of signs to analyze these zeroes.

Note: It is essential to know how to solve the polynomial equation for its roots. We can use many methods and the best-known method is factorization. The above equation in the given question cannot be factorized and therefore we need to use any alternative method to solve this.