Solveeit Logo
Login

Question

Question: How do you find all the asymptotes for the function \[g\left( x \right)={{e}^{x-2}}\]?...

How do you find all the asymptotes for the function g(x)=ex−2g\left( x \right)={{e}^{x-2}}?

Explanation

Solution

This question is from the topic of pre-calculus. In this question, we have to find the asymptotes of a given function. In solving this question, we will first understand about all the asymptotes: vertical asymptote, horizontal asymptote and oblique asymptote. After that, we will find out all the asymptotes that are possible from the given function. After that, we get our answer.

Complete step-by-step solution:
Let us solve this question.
In this question, we have asked to find all the asymptotes of the function given in the question.
The function given in the question is:
g(x)=ex−2g\left( x \right)={{e}^{x-2}}
Before solving this question, let us first know about the asymptotes that are horizontal asymptote, vertical asymptote and oblique asymptote.
Horizontal asymptote: This asymptote gives the value of y for which the curve or graph of any rational function approaches to x at infinity or negative of infinity. This asymptote is in the form of x=a, where a is any constant.
Vertical asymptote: This asymptote gives the value of x for which the curve or graph of any rational function approaches to y at infinity or negative of infinity. This asymptote is in the form of y=b, where b is any constant.
Oblique asymptote: This asymptote gives the value x and y when the graph of any rational function approaches x at infinity or negative of infinity and also y at infinity or negative of infinity. This asymptote is in the form of line y=mx+c, where, m is not zero.
Now, let us see the graph for the function g(x)=ex−2g\left( x \right)={{e}^{x-2}} to understand its asymptotes:

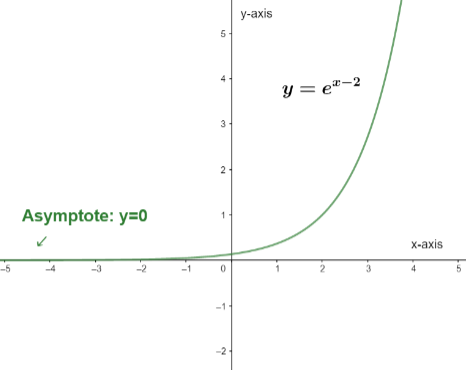
Here, we can see that there is a horizontal asymptote as it is reaching the x at negative of infinity. The asymptote is: y=0.

Note: We should have a better knowledge in the topic of asymptote to solve this type of question easily. We should know about all types of asymptotes : horizontal asymptote, vertical asymptote, and oblique asymptote. Remember that the distance between the curve and the asymptote tends to zero as they head to infinity or negative of infinity.