Question
Question: How do you find all solutions of the equation \(\sec x+\tan x=1\) in the interval \(\left[ 0,2\pi \r...
How do you find all solutions of the equation secx+tanx=1 in the interval [0,2π)?
Solution
In this problem we need to calculate all the solutions of the given equation which is secx+tanx=1. For solving this we are going to use the trigonometric identity which is sec2x−tan2x=1. We can simplify this identity by using the formula a2−b2=(a+b)(a−b). Here we will use the given equation secx+tanx=1 and calculate the value of secx−tanx. From the values of secx+tanx and secx−tanx we will calculate the value of secx by adding both the values. After that we will use the basic trigonometric definition of secx which is secx=cosx1 to calculate the value of cosx. From this we can write the general solution of the equation and from the general solution we can calculate the solutions which are in the given interval [0,2π).
Complete step by step answer:
Given equation, secx+tanx=1.
We have the trigonometric identity sec2x−tan2x=1. Applying the formula a2−b2=(a+b)(a−b) in the trigonometric identity, then we will get
(secx+tanx)(secx−tanx)=1
Substituting the value secx+tanx=1 in the above equation and simplifying it, then we will have
1(secx−tanx)=1⇒secx−tanx=1
We have the values secx+tanx=1, secx−tanx=1. Adding both the values to get the value of secx, then we will get
secx+tanx+(sec−tanx)=1+1
Simplifying the above equation by using mathematical operations, then we will get
secx+tanx+secx−tanx=2⇒2secx=2⇒secx=1
From basic definitions of trigonometry, we have the formula secx=cosx1. Substituting this value in the above equation, then we will get
cosx1=1⇒cosx=1
We have the trigonometric value cos0∘=1. Substituting this value in the above equation, then we will have
cosx=cos0∘
We can write the general solution of the equation cosx=cosθ as x=2kπ±θ, k∈Z. So, the general solution of the equation cosx=cos0∘ will be
x=2kπ±0⇒x=2kπ, k∈Z.
Now substitute k=0,1,2,... in the general solution to get the solutions of the given equation, then we will get
x=0,2π,4π,...
The solutions of the given equation secx+tanx=1 lies in the interval [0,2π) is only 0.
Note: We can also plot the graph of the given equation and observe the solution of the given equation in the given interval. The graph of the given equation secx+tanx=1 will be
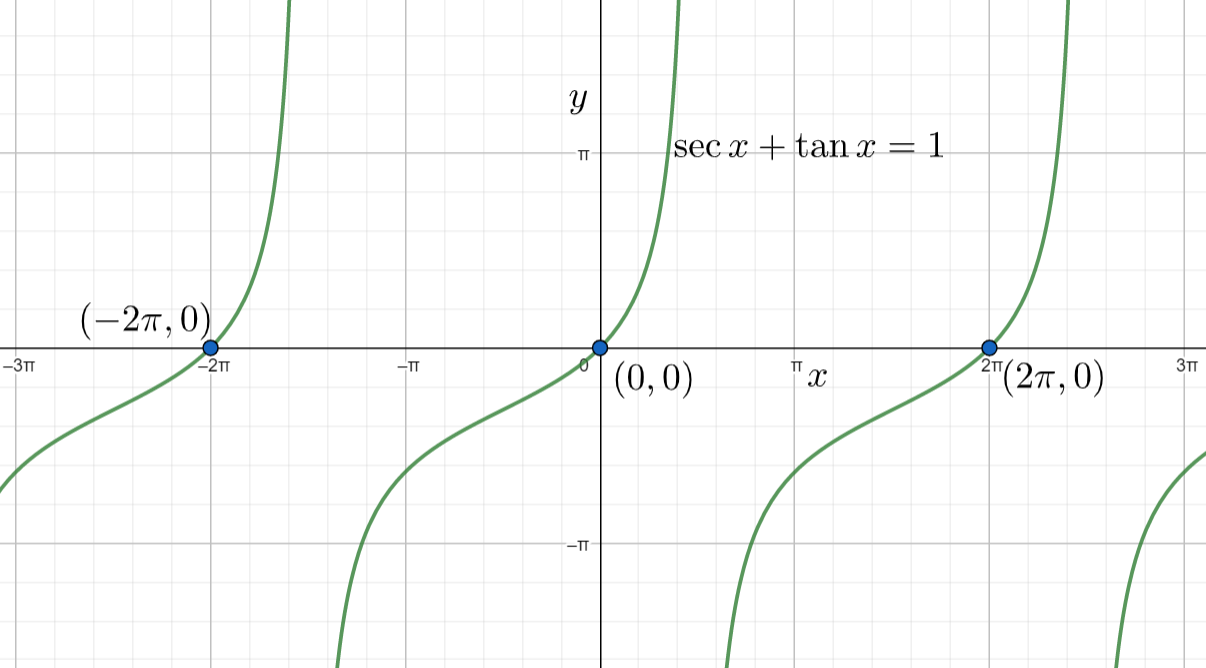
From the above graph also, we can observe that the solution of the given equation in the given interval is 0 only. In the interval they have included the value of 0 but not the value of 2π, so we are not considering the value of 2π as a solution in the given interval.
