Question

How do you find all solutions between 0 to $2\pi$ for $4{{\sin }^{2}}x-3=0$ ?

Answer 1

In the equation $4{{\sin }^{2}}x-3=0$ first we will find the value of sin x and then we will check that value whether that value lie in the range of sin x , we know that range of sin x is from -1 to 1 . If the roots come in the range of sin x then we will solve for x by using graphs.

Complete step by step answer:
The given equation in the question is $4{{\sin }^{2}}x-3=0$ we have found all values of x that satisfy the equation and are between 0 to $2\pi$ .
First let’s find the value of sin x that satisfy the equation
Let’s add 3 in both LHS and RHS , by adding 3 both sides we get
$4{{\sin }^{2}}x=3$
Diving LHS and RHS by 4 we get
${{\sin }^{2}}x=\dfrac{3}{4}$
So the value of sin x is $\pm \dfrac{\sqrt{3}}{2}$
So we have find the value of x for which sin x is equal to $\dfrac{\sqrt{3}}{2}$ and sin x is $-\dfrac{\sqrt{3}}{2}$
Let’s solve this by graph

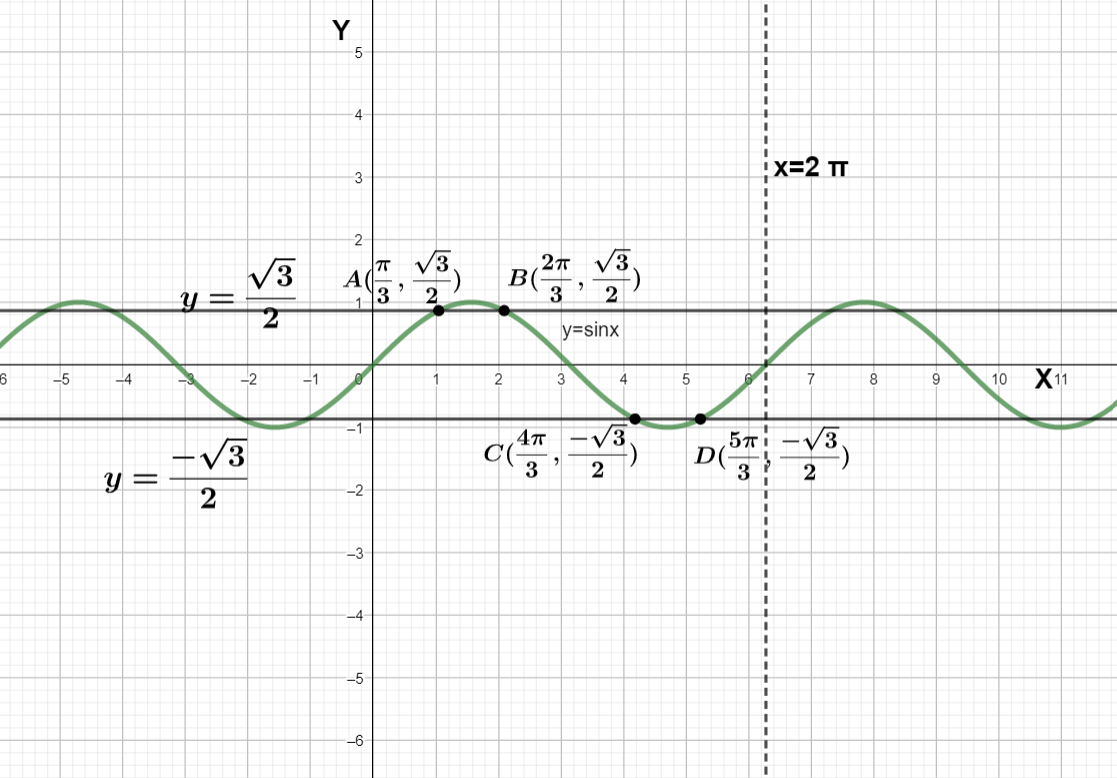
We can see the point of intersection the 2 line with y= sin x are A , B, C, and D
So all the solutions from 0 to $2\pi$ are $\dfrac{\pi }{3}$ , $\dfrac{2\pi }{3}$ , $\dfrac{4\pi }{3}$ and $\dfrac{5\pi }{3}$

Note:
We can check all the solutions whether these are correct or not by putting the value of x in the equation. When we put $\dfrac{\pi }{3}$ or $\dfrac{2\pi }{3}$ in the equation $4{{\sin }^{2}}x-3=0$ the result came out to be $4{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}-3$ which is equal to 0 , so $\dfrac{\pi }{3}$ and $\dfrac{2\pi }{3}$ are correct answers. When we put $\dfrac{4\pi }{3}$ or $\dfrac{5\pi }{3}$ we get $4{{\left( -\dfrac{\sqrt{3}}{2} \right)}^{2}}-3$ which is equal to 0, so $\dfrac{4\pi }{3}$ and $\dfrac{5\pi }{3}$ are correct answers.