Question

How do you find all six trigonometric functions of $\theta$ if the point $\left( { - 1, - 2} \right)$ is on the terminal side of $\theta$ ?

Answer 1

Hint : Draw the point on the graph and then join the points straight and from the centre. Will get $- 1$ as base $- 2$ as height and terminal side $\theta$ . According to the heights and base obtained we can write all the six formulas of trigonometry.

Complete step by step solution:
We are given the points $\left( { - 1, - 2} \right)$ which is on the terminal side of $\theta$ .Draw the point on the graph. Now, according to the points we can see that the graph is in the 3rd Quadrant.
Let’s draw the picture accordingly and we get:

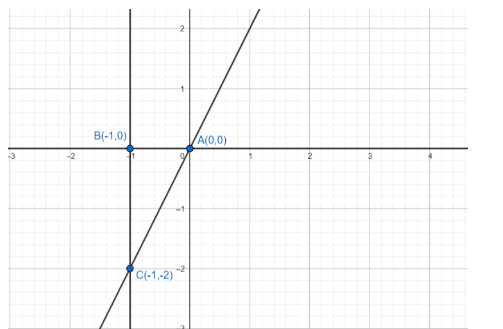
So, we can see that the y-coordinate is at distance $2$ , so for the $\vartriangle ABC$ perpendicular becomes $2$ which is BC and base becomes $1$ which is AB. Let’s calculate the hypotenuse AC.
Using Pythagoras-Theorem we write:
${\left( {AB} \right)^2} + {\left( {BC} \right)^2} = {\left( {AC} \right)^2} \\\ {\left( 1 \right)^2} + {\left( 2 \right)^2} = {\left( {AC} \right)^2} \\\ 1 + 4 = {\left( {AC} \right)^2} \\\ 5 = {\left( {AC} \right)^2} \\\ AC = \sqrt 5 \;$
Since, the triangle is in the third quadrant so its angle. Therefore, the trigonometric values would be all negative except $\tan \theta$ and $\cot \theta$ as it is the quadrant for these two and the rest else are having negative values.
So, according to this all the three trigonometric values, which has a point $\left( { - 1, - 2} \right)$ is on the terminal side of $\theta$ are given as:
$\sin \theta = \dfrac{p}{h} = - \dfrac{2}{{\sqrt 5 }}$
$\cos \theta = \dfrac{b}{h} = - \dfrac{1}{{\sqrt 5 }}$
$\tan \theta = \dfrac{p}{b} = \dfrac{2}{1} = 2$
$\cot \theta = \dfrac{1}{{\tan \theta }} = \dfrac{1}{2}$
$\sec \theta = \dfrac{h}{b} = - \dfrac{{\sqrt 5 }}{1}$
$\cos ec\theta = \dfrac{h}{p} = - \dfrac{{\sqrt 5 }}{2}$

Note : Always check for the quadrant in which quadrant the point lies according to the question, before coming to finding the trigonometric values.
There can be an error in determining the signs of the trigonometric values, so remember that the signs of the trigonometric values are always according to their quadrants in which the point lies.