Question

How do you find all $\dfrac{\cos 2x}{\sin 3x-\sin x}$ in the interval $\left[ 0,2\pi \right)$ ?

Answer 1

Firstly, we simplify the above trigonometric function, especially the denominator using trigonometric identities and formula. After evaluating we get simpler trigonometric terms for whom we find the solutions in the range $\left[ 0,2\pi \right)$ .

Complete step-by-step solution:
The given trigonometric function is $y=\dfrac{\cos 2x}{\sin 3x-\sin x}$
Consider the denominator $\sin 3x-\sin x$
We now simplify this using the trigonometric identity which is,
$\sin A-\sin B=2\cos \left( \dfrac{A+B}{2} \right)\sin \left( \dfrac{A-B}{2} \right)$
$\Rightarrow \sin 3x-\sin x=2\cos \left( \dfrac{3x+x}{2} \right)\sin \left( \dfrac{3x-x}{2} \right)$
On further evaluating we get,
$\Rightarrow 2\cos \left( \dfrac{4x}{2} \right)\sin \left( \dfrac{2x}{2} \right)$
$\Rightarrow 2\cos \left( 2x \right)\sin \left( x \right)$
Now substitute this back into our equation and rewrite the terms accordingly.
$\Rightarrow y=\dfrac{\cos 2x}{2\cos \left( 2x \right)\sin \left( x \right)}$
Now rearrange the terms,
$\Rightarrow y=\dfrac{1}{2}\left( \dfrac{\cos 2x}{\cos 2x} \right)\left( \dfrac{1}{\sin \left( x \right)} \right)$
We can further represent one of the terms as, $\dfrac{1}{\sin \left( x \right)}=\cos ecx$
Hence $\dfrac{1}{2}\cos ecx,\cos 2x\ne 0$
Writing the general equation for $coes2x\ne 0$
Here, $2x\ne \left( 2n+1 \right)\dfrac{\pi }{2};n=0,\pm 1,\pm 2.....$
$\Rightarrow x\ne \left( 2n+1 \right)\dfrac{\pi }{4}$
Now we know that $\dfrac{1}{2}\cos ecx\notin \dfrac{1}{2}\left( -1,1 \right)=\left( -\dfrac{1}{2},\dfrac{1}{2} \right)$
Now let us substitute the values to get the solutions.
For $n=0$ ; $x\ne \dfrac{\pi }{4}$
For $n=1$ ; $x\ne \dfrac{3\pi }{4}$
For $n=2$ ; $x\ne \dfrac{5\pi }{4}$
For $n=3$ ; $x\ne \dfrac{7\pi }{4}$
Hence all the values except $\dfrac{\pi }{4},\dfrac{3\pi }{4},\dfrac{5\pi }{4},\dfrac{7\pi }{4}$ are the solution for the trigonometric expression.
The graph for the trigonometric function is as follows.

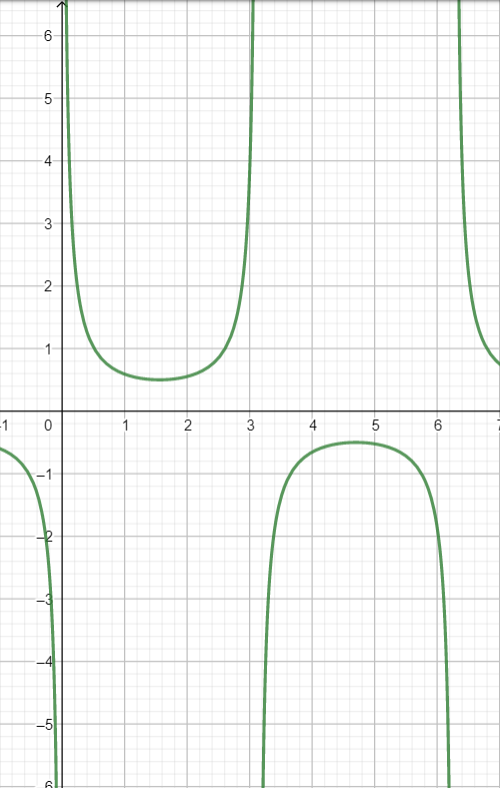
Note: Whenever complex equations are given to solve one must always Firstly start from the complex side and then convert all the terms into $\sin \theta$ or $\cos \theta$ . Then combine them into single fractions. Now it is most likely to use Trigonometric identities for the transformations if there are any.
Know when and where to apply the Subtraction-Addition formula. Must check where the Trigonometric functions become negative in which Quadrant to easily find the values in the given range.