Question

How do you find a vertical asymptote for $y=\sec \left( x \right)$?

Answer 1

The asymptote of a function is a line to which the graph of the function approaches when one or both of the x and y coordinates approaches infinity. In the above question, we are asked to find the vertical asymptote for the function $y=\sec \left( x \right)$. The vertical asymptote means that only the y coordinate will approach infinity when the x coordinate approaches a finite value. For this we need to determine the value of x for which the function $y=\sec \left( x \right)$ approaches infinity. Since $\cos \left( x \right)=\dfrac{1}{\sec \left( x \right)}$, $\cos \left( x \right)$ will approach zero. From this, all the vertical asymptotes can be determined.

Complete step by step solution:
We know that the asymptote of a function is a line to which the graph of the function approaches when one or both of the x and y coordinate approaches infinity. But since we are asked to determine the vertical asymptote, the y coordinate must tend to infinity for a particular value of the x coordinate. According to the above question $y=\sec \left( x \right)$, which means that $\sec \left( x \right)$ will approach infinity. Also, we know that $\cos \left( x \right)=\dfrac{1}{\sec \left( x \right)}$. So as $\sec \left( x \right)$ will approach infinity, $\cos \left( x \right)$ will approach zero. So we consider the equation
$\Rightarrow \cos \left( x \right)=0$
We know that the general solution of the above equation is given by
$\Rightarrow x=\dfrac{\left( 2n+1 \right)\pi }{2}$
So the vertical asymptotes of the given function are $x=\pm \dfrac{\pi }{2},\pm \dfrac{3\pi }{2},\pm \dfrac{5\pi }{2}......$
We can observe these asymptotes in the below graph.

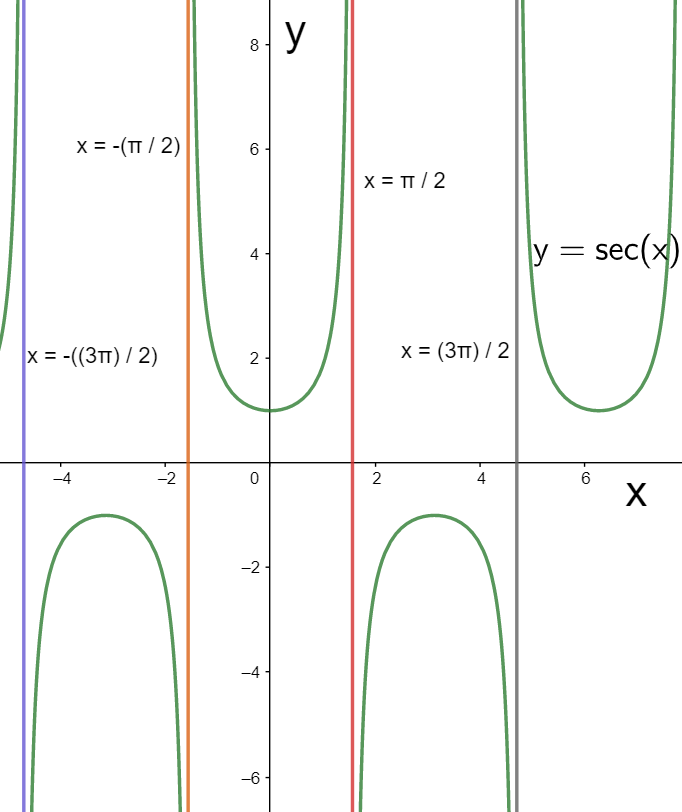
Hence, we have determined the vertical asymptotes of the given function.

Note: We must note from the above graph of the function $y=\sec \left( x \right)$ that only the vertical asymptotes exist for it. Since the secant function is a trigonometric function, it is periodic and therefore no horizontal asymptote will exist for it. The asymptote of the given function are determined as $x=\pm \dfrac{\pi }{2},\pm \dfrac{3\pi }{2},\pm \dfrac{5\pi }{2}......$. These values can also be termed as the points of discontinuities for the given function, as can be seen in the above graph. Therefore for determining the vertical asymptotes of a trigonometric function, we just have to find out its points of discontinuities.