Solveeit Logo
Login

Question

Question: How do you find a standard form equation for the line with slope \(\dfrac{2}{3}\) that passes throug...

How do you find a standard form equation for the line with slope 23\dfrac{2}{3} that passes through the point (3,6)\left( 3,6 \right)?

Explanation

Solution

In this problem we need to calculate the equation of the line which is having the slope 23\dfrac{2}{3} and passes through the point (3,6)\left( 3,6 \right). We have the formula for the equation of the line having slope mm and passes through a point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) as (y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right). So, we will substitute all the values we have in the above equation and simplify the obtained equation by using the distribution law of multiplication over subtraction. After simplifying the equation, we will get our required solution.

Complete answer:
Given that the line has slope 23\dfrac{2}{3}.
⇒m=23\Rightarrow m=\dfrac{2}{3}
Now the line passes through the point (3,6)\left( 3,6 \right)
⇒(x1,y1)=(3,6)\Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,6 \right)
We know that the equation of the line having slope mm and passes through a point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is
(y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)
Substituting the values of mm, x1{{x}_{1}}, y1{{y}_{1}} in the above equation, then we will get
⇒(y−6)=23(x−3)\Rightarrow \left( y-6 \right)=\dfrac{2}{3}\left( x-3 \right)
Doing cross multiplication in the above equation, then we will get
⇒3(y−6)=2(x−3)\Rightarrow 3\left( y-6 \right)=2\left( x-3 \right)
From the distribution law of multiplication over subtraction we have a(b−c)=ab−aca\left( b-c \right)=ab-ac. Applying this law in the above equation, then we will get
⇒3×y−3×6=2×x−2×3 ⇒3y−18=2x−6 \begin{aligned} & \Rightarrow 3\times y-3\times 6=2\times x-2\times 3 \\\ & \Rightarrow 3y-18=2x-6 \\\ \end{aligned}
Shifting the term 3y−183y-18 which is on the left hand side to right hand side. When there is a shifting from one side to another side is takes place there should be change of sign also takes place, then we will get
⇒2x−6−3y+18=0\Rightarrow 2x-6-3y+18=0
Simplifying and rearranging the term in the above equation, then we will get the equation of the required line as
∴2x−3y+12=0\therefore 2x-3y+12=0
And the graph of the above line will be

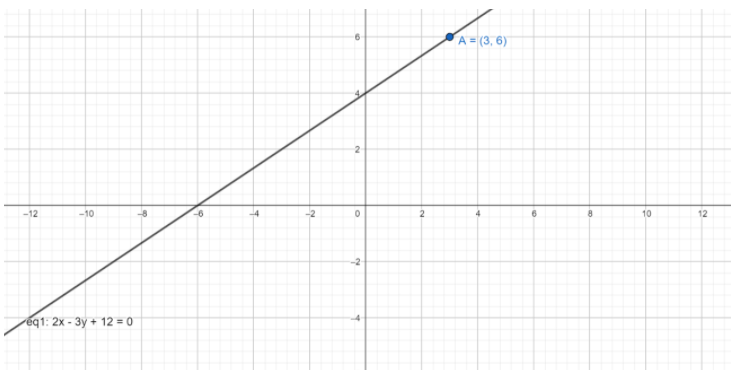
Note: We can also check that whether the obtained equation is correct or wrong by substituting the given point in the obtained equation. Then we will get
⇒2(3)−3(6)+12=0 ⇒6−18+12=0 ⇒−18+18=0 ⇒0=0 ⇒LHS=RHS \begin{aligned} & \Rightarrow 2\left( 3 \right)-3\left( 6 \right)+12=0 \\\ & \Rightarrow 6-18+12=0 \\\ & \Rightarrow -18+18=0 \\\ & \Rightarrow 0=0 \\\ & \Rightarrow LHS=RHS \\\ \end{aligned}
Hence the obtained equation is correct.