Question

How do you find a formula for the linear function with slope $-5$ and x-intercept $8$?

Answer 1

The slope and the x-intercept of the linear function are given to be equal to $-5$ and $8$ respectively. We know that the slope and the intercept are defined for a line. So this means that we have to deduce the equation of the line having the characteristics given in the above question. The x-intercept of $8$ means that the line must pass through the point $\left( 8,0 \right)$. On putting the slope $m=-5$, and the point ${{x}_{1}}=8$,${{y}_{1}}=0$ in the point slope form of a line, given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$, we will obtain the required linear function.

Complete step by step solution:
The linear function refers to expressing $y$ in terms of the linear power of $x$. We know that such a relation is nothing but the equation of a line.
In the above question, we are given the slope of the linear function as $m=-5$. Also, the x-intercept of the linear function is given to be equal to $8$. This means that the point $\left( 8,0 \right)$ must satify the linear function, or the line. So we have a point and the slope of the line. From the point slope form of a line, we have
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Substituting ${{x}_{1}}=8$,${{y}_{1}}=0$ and $m=-5$ in the above equation, we get
$\begin{aligned} & \Rightarrow y-0=-5\left( x-8 \right) \\\ & \Rightarrow y=-5x+40 \\\ \end{aligned}$
The graph for this linear function is given below.

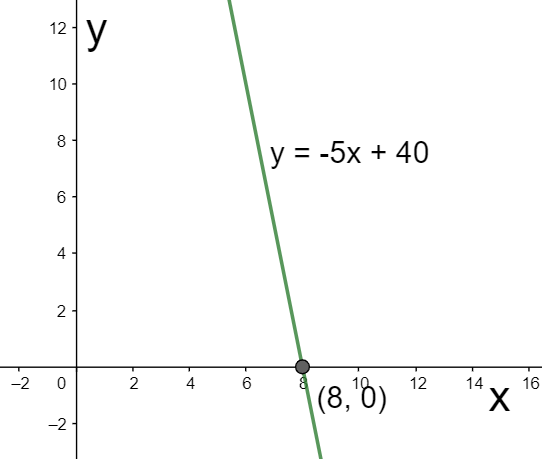
Hence, we have found the required formula for the linear function as $y=-5x+40$.

Note:
In the given question, we were given the slope and an intercept for the linear function. Do not use the slope intercept form of the line given by $y=mx+c$ since this form is for the y-intercept, while we were given the x-intercept. Also, after obtaining the linear function, check for the values of the slope and the x-intercept from the final equation obtained.