Solveeit Logo
Login

Question

Question: How do you factor \[{x^3} - {x^2} + x - 6 = 0\] ?...

How do you factor x3−x2+x−6=0{x^3} - {x^2} + x - 6 = 0 ?

Explanation

Solution

This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. Also, we need to know how to multiply xx the term with the constant term, xx a term with thexx term, and the constant term with the constant term. Also, we need to know the substitution process to solve this question. The final answer would be a simplified form of the given equation.

Complete step by step solution:
The given equation is shown below,
x3−x2+x−6=0→(1){x^3} - {x^2} + x - 6 = 0 \to \left( 1 \right)
For solving the above equation we can assume
x=...−2,−2,0,1,2,....x = ... - 2, - 2,0,1,2,....
To find the first factor of the given equation, let’s try x=1x = 1
(1)→x3−x2+x−6=0\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0

(1)3−(1)2+1−6=0 1−1+1−6=0 \-5≠0 {\left( 1 \right)^3} - {\left( 1 \right)^2} + 1 - 6 = 0 \\\ 1 - 1 + 1 - 6 = 0 \\\ \- 5 \ne 0 \\\

So, x=1x = 1 is not a factor of the given equation.
Let’s try x=2x = 2
(1)→x3−x2+x−6=0\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0

(2)3−(2)2+2−6=0 8−4+2−6=0 8−8=0 0=0 {\left( 2 \right)^3} - {\left( 2 \right)^2} + 2 - 6 = 0 \\\ 8 - 4 + 2 - 6 = 0 \\\ 8 - 8 = 0 \\\ 0 = 0 \\\

So, x=2x = 2 is a factor of the given equation.
So, the equation (1)\left( 1 \right) can also be written as,
(1)→x3−x2+x−6=0\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0
(x−2)(?)=0→(2)\left( {x - 2} \right)\left( ? \right) = 0 \to \left( 2 \right)
Here, the first factor is known, so we would find the second factor of the given equation.
From the equations (1)\left( 1 \right) and (2)\left( 2 \right), we get
x3−x2+x−6=(x−2)(?)=0→(3){x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( ? \right) = 0 \to \left( 3 \right)
First, we need to build x3{x^3}
So, we write

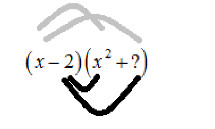
It gives x3{x^3}. But −2×x2 - 2 \times {x^2}gives−2x2 - 2{x^2}
So, we get
(x−2)(x2+?)=x3−2x2+?\left( {x - 2} \right)\left( {{x^2} + ?} \right) = {x^3} - 2{x^2} + ?
Next, we need to build −x2 - {x^2}, already we have −2x2 - 2{x^2}. So, if we put x2{x^2} we get,
−2x2+x2=−x2- 2{x^2} + {x^2} = - {x^2}
So, we get

(x−2)(x2+x+?)=x3−2x2+x2−2x+? (x−2)(x2+x+?)=x3−x2−2x+? \left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - 2{x^2} + {x^2} - 2x + ? \\\ \left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - {x^2} - 2x + ? \\\

Next, we need to buildxx. We already have −2x - 2x. So, we put 3x3x
−2x+3x=x- 2x + 3x = x
So, we get

(x−2)(x2+x+3+?)=x3−x2−2x+3x−6 (x−2)(x2+x+3+?)=x3−x2+x−6 \left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} - 2x + 3x - 6 \\\ \left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} + x - 6 \\\

Next, we need to build −6 - 6. We already have −6 - 6
So, we get
\left( {x - 2} \right)\left( {{x^2} + x + 3} \right) = {x^3} - {x^2} + x - 6$$$$ \to \left( 4 \right)
By comparing the equation (3)\left( 3 \right)and(4)\left( 4 \right), we get
x3−x2+x−6=(x−2)(x2+x+3){x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)
So, finally, we get the second factor as,
(x2+x+3)\left( {{x^2} + x + 3} \right)
We can’t simplify the term further.
So, the final answer is,
x3−x2+x−6=(x−2)(x2+x+3){x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)

Note: This question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. Note that for finding the first factor in these types of questions we have to assume the xx values and check them with the given equation. If thexxvalue satisfies the given equation we can take it as one of the factors of the given equation.