Question

How do you factor ${x^3} - {x^2} - 4x + 4$?

Answer 1

To order to determine the factors of the above cubic equation first pick our common from first two terms and last two and use the formula $\left( {{A^2} - {B^2}} \right) = \left( {A - B} \right)\left( {A + B} \right)$to find all the factors .

Complete step by step solution:
Given a Cubic equation${x^3} - {x^2} - 4x + 4$,let it be $f(x)$
$f(x) = {x^3} - {x^2} - 4x + 4$
Comparing the equation with the standard cubic equation $a{x^3} + b{x^2}cx + d$
a becomes 1
b becomes -1
c becomes -4
and d becomes 4
To find the cubic factorization,
Taking common ${x^2}$from the first two terms and $- 4$from the last two terms
$f(x) = {x^2}(x - 1) - 4(x - 1) \\\ = (x - 1)({x^2} - 4) \\\ = (x - 1)({x^2} - {2^2}) \\\$Again pull out common$(x - 1)$ from both the terms .
Consider $x$as A and $2$as B and Applying Identity $\left( {{A^2} - {B^2}} \right) = \left( {A - B} \right)\left( {A + B} \right)$
Now our equation becomes
$f\left( x \right) = (x - 1)(x - 2)(x + 2)$
Hence, we have successfully factorized our cubic equation.
Therefore, the factors are $(x - 1)(x - 2)(x + 2)$

Additional Information:
Cubic Equation: A cubic equation is a equation which can be represented in the form of $a{x^3} + b{x^2}cx + d$where $x$is the unknown variable and a,b,c,d are the numbers known where $a \ne 0$.If $a = 0$then the equation will become a quadratic equation and will no longer be cubic.
The degree of the quadratic equation is of the order 3.
Every Cubic equation has 3 roots.
The Graph of any cubic polynomial is symmetric with respect to the inflection point of the
polynomial.
Graph to cubic polynomial $y = {x^3} - {x^2} - 4x + 4$

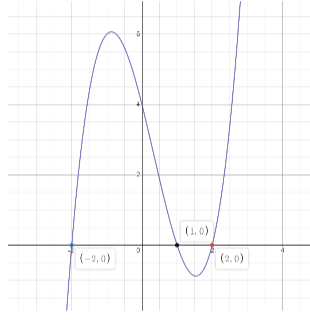
The points at which the graph touches the x-axis are the roots of the polynomial.

Note: 1. One must be careful while calculating the answer as calculation error may come.
2.Don’t forget to compare the given cubic equation with the standard one every time.