Solveeit Logo
Login

Question

Question: How do you express \(\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right...

How do you express sin⁡(sin⁡−1(x)+cos⁡−1(y))\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right) without trigonometric function?

Explanation

Solution

Here, in the given question, we need to express sin⁡(sin⁡−1(x)+cos⁡−1(y))\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right) without trigonometric function. As we can see sin⁡(sin⁡−1(x)+cos⁡−1(y))\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right) is given in the form of an identity sin⁡(A+B)=sin⁡Acos⁡B+cos⁡Asin⁡B\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B, so we will try to expand the given expression using this identity. After that we will use Pythagoras theorem to express functions in the form which is without any trigonometric function to get our required answer.

Formulae used:
sin⁡(A+B)=sin⁡Acos⁡B+cos⁡Asin⁡B\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B
⇒sin⁡(sin⁡−1x)=x\Rightarrow \sin \left( {{{\sin }^{ - 1}}x} \right) = x
⇒cos⁡(cos⁡−1y)=y\Rightarrow \cos \left( {{{\cos }^{ - 1}}y} \right) = y

Complete step by step answer:
Given, sin⁡(sin⁡−1(x)+cos⁡−1(y))\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)
As we know, sin⁡(A+B)=sin⁡Acos⁡B+cos⁡Asin⁡B\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B
Let A=sin⁡−1xA = {\sin ^{ - 1}}x and B=cos⁡−1yB = {\cos ^{ - 1}}y.
⇒sin⁡(sin⁡−1x+cos⁡−1y)=sin⁡(sin⁡−1x)cos⁡(cos⁡−1y)+cos⁡(sin⁡−1x)sin⁡(cos⁡−1y)\Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = \sin \left( {{{\sin }^{ - 1}}x} \right)\cos \left( {{{\cos }^{ - 1}}y} \right) + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right)
As we know, sin⁡(sin⁡−1x)=x\sin \left( {{{\sin }^{ - 1}}x} \right) = x and cos⁡(cos⁡−1y)=y\cos \left( {{{\cos }^{ - 1}}y} \right) = y. Therefore, we get
⇒sin⁡(sin⁡−1x+cos⁡−1y)=xy+cos⁡(sin⁡−1x)sin⁡(cos⁡−1y).....(i)\Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right).....\left( i \right)
Now, we will solve cos⁡(sin⁡−1x)\cos \left( {{{\sin }^{ - 1}}x} \right) and sin⁡(cos⁡−1y)\sin \left( {{{\cos }^{ - 1}}y} \right) individually.
We have to find the value of cos⁡(sin⁡−1x)=cos⁡(sin⁡−1x1)\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( {{{\sin }^{ - 1}}\dfrac{x}{1}} \right). As we know sin⁡θ=PH\sin \theta = \dfrac{P}{H}, from here we will find the value of base.
The right triangle with perpendicular = xx and hypotenuse = 11. Therefore,

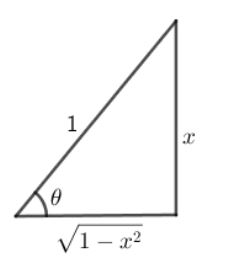
Base=H2−P2Base = \sqrt {{H^2} - {P^2}}
Base = 1−x2\sqrt {1 - {x^2}} .
Therefore, we get
⇒sin⁡−1x=cos⁡−11−x21\Rightarrow {\sin ^{ - 1}}x = {\cos ^{ - 1}}\dfrac{{\sqrt {1 - {x^2}} }}{1}.
Hence, cos⁡(sin⁡−1x)=cos⁡(cos⁡−11−x21)\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( {{{\cos }^{ - 1}}\dfrac{{\sqrt {1 - {x^2}} }}{1}} \right)
⇒cos⁡(sin⁡−1x)=1−x2\Rightarrow \cos \left( {{{\sin }^{ - 1}}x} \right) = \sqrt {1 - {x^2}}
Now, we will find the value of sin⁡(cos⁡−1y)=sin⁡(cos⁡−1y1)\sin \left( {{{\cos }^{ - 1}}y} \right) = \sin \left( {{{\cos }^{ - 1}}\dfrac{y}{1}} \right). As we know cos⁡θ=BH\cos \theta = \dfrac{B}{H}, from here we will find the value of perpendicular.
The right triangle with base = yy and hypotenuse = 11. Therefore,

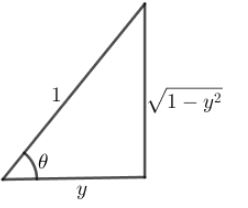
Perpendicular=H2−B2Perpendicular = \sqrt {{H^2} - {B^2}}
Perpendicular = 1−y2\sqrt {1 - {y^2}}
Therefore, we get
⇒cos⁡−1y=sin⁡−11−y21\Rightarrow {\cos ^{ - 1}}y = {\sin ^{ - 1}}\dfrac{{\sqrt {1 - {y^2}} }}{1}.
Hence, sin⁡(cos⁡−1x)=sin⁡(sin⁡−11−y21)\sin \left( {{{\cos }^{ - 1}}x} \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{{\sqrt {1 - {y^2}} }}{1}} \right)
⇒sin⁡(cos⁡−1x)=1−y2\Rightarrow \sin \left( {{{\cos }^{ - 1}}x} \right) = \sqrt {1 - {y^2}}
Now, we will substitute value of cos⁡(sin⁡−1x)\cos \left( {{{\sin }^{ - 1}}x} \right) and sin⁡(cos⁡−1y)\sin \left( {{{\cos }^{ - 1}}y} \right) in (i)\left( i \right).
sin⁡(sin⁡−1x+cos⁡−1y)=xy+cos⁡(sin⁡−1x)sin⁡(cos⁡−1y).....(i)\sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right).....\left( i \right)
⇒sin⁡(sin⁡−1x+cos⁡−1y)=xy+1−x2×1−y2\Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \sqrt {1 - {x^2}} \times \sqrt {1 - {y^2}}

Therefore, we can write sin⁡(sin⁡−1(x)+cos⁡−1(y))\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right) without trigonometric functions as xy+1−x2×1−y2xy + \sqrt {1 - {x^2}} \times \sqrt {1 - {y^2}} .

Note: Remember that inverse trigonometric functions do the opposite of the regular trigonometric functions. For example: inverse sin⁡e\sin e i.e., sin⁡−1{\sin ^{ - 1}} does the opposite of sine. The expression sin⁡−1x{\sin ^{ - 1}}x is not the same as 1sin⁡x\dfrac{1}{{\sin x}}. In other words, the −1 - 1 is not an exponent. Instead, it simply means inverse function.