Question

How do you experimentally find the refractive index of the material of prism?

Answer 1

You can start by explaining the apparatus needed for the experiment. Then explain how to calculate the value of the angle of deviation and the value of the angle of the prism. Then use the equation $\mu = \dfrac{{\sin \left[ {\dfrac{{(A + D}}{2}} \right]}}{{\sin \dfrac{A}{2}}}$ to reach the solution.

Complete answer:
For determining the refractive index of the material of a prism you need the following material: A prism, piece of white chart or a white sheet, pins, scale, and a protractor.

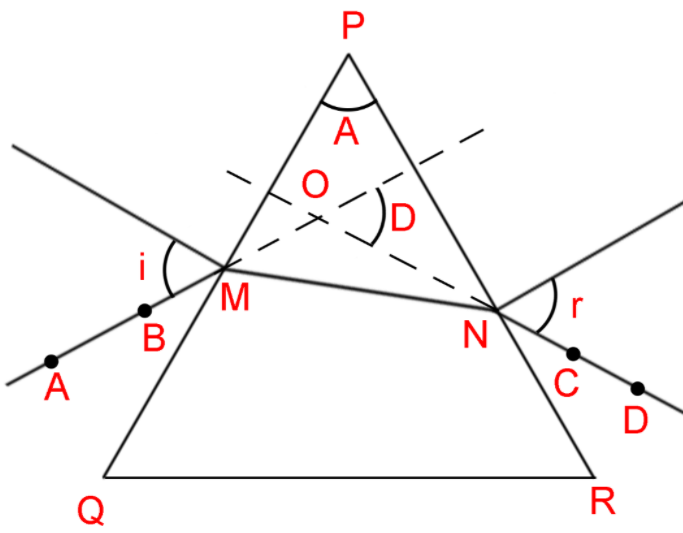
Place the prism on the white chart in such a way that the triangular base of the prism is in contact with the chart.
Outline the triangular base of the prism on the white chart.
We obtain a triangle on the sheet, let’s name its vertices $P$ , $Q$ and $R$ .
Now, measure the angle between lines $PQ$ and $PR$ , let’s call this $\angle A$ .
Mark a point $M$ on the side $PQ$ of the triangle (preferably on the center) and also draw a line perpendicular to $PQ$ passing through the point $M$ .
Keep the center of the protractor at the point $M$ make a point $A$ at an angle of $30^\circ$ . Join the point $A$ with the point $M$ .
Then place the prism back in its position on the white chart
Then place a pin at point $A$ and one at a point $B$ on the line $AM$ .
Then look at the images from the opposite side of the prism and place two new pins in such a way that the 4 pins line up in a straight line.
Remove the pins and the prism and let’s name the two new points on the chart $C$ and $D$ respectively. Draw a line along with the points $C$ and $D$ till it meets the surface of the line $PR$ . Let the point where it meets the line $PR$ to be $N$.
Draw a line at the point $N$ perpendicular to the line $PR$ .
Extend both line $AM$ and line $DN$ till they intersect at the point $O$ .
The $\angle i$ and $\angle r$ in the figure represent the angle of incidence and the angle of emergence respectively.
The angle $\angle D$ in the figure represents the angle of deviation ( the angle that the incident ray makes with the emergent ray)
Calculations –
The refractive index of the material of the prism is calculated by using the following formula
$\mu = \dfrac{{\sin \left[ {\dfrac{{(A + D}}{2}} \right]}}{{\sin \dfrac{A}{2}}}$

Note:
In the solution above we only calculated the refractive index of the prism by keeping the angle of incidence as $30^\circ$ , but it is common practice to take multiple angles of incidence and then follow the above process again and again. This gives us multiple values of the refractive index of the material of the prism. The average of these values will give us a more precise value of the refractive index.