Question
Question: How do you expand \({\left( {x - 5} \right)^6}\) using Pascal’s triangle?...
How do you expand (x−5)6 using Pascal’s triangle?
Solution
We first write the binomial expansion of (x−5)6. Then we explain Pascal's triangle and the use it. We explain how the coefficients work. We also explain the use of the constant a and n in the general expansion of (x+a)n. Then we find the coefficients of the equation (x−5)6 using Pascal’s triangle.
Complete step-by-step answer:
First, we write down the binomial expansion of the given equation (x−5)6, then we explain it with the help of Pascal’s triangle.
⇒(x−5)6=x6−30x5+375x4−2500x3+9375x2−18750x+15625
Pascal’s triangle helps to find the coefficients for the expansion of the (x−5)6, where n decides the number of times, we continue with the triangle expansion and the added value with x (for general case a) decides the multiplier. We multiply with an, a=0(1)n consecutively.
We first draw the triangle values till the 7th row where it starts with 1 at the top.
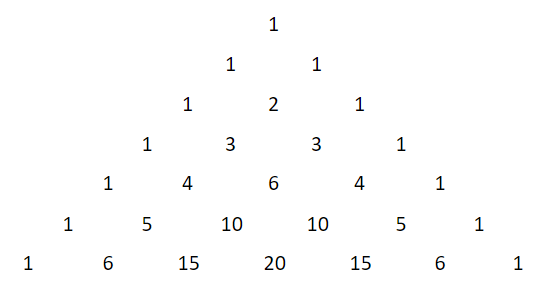
Every coefficient is the addition of the previous two coefficients on its top. These coefficients are made for the expansion of the term (x+1)n. For particular we took the value of n=6 and that’s why we took 6 rows after the first value of 1 at the top.
Now instead of a, we have to multiply with -5 as for the equation (x−5)6 we have a=−5.
The relative coefficients are 1, 6, 15, 20, 15, 6 ,1. We multiply them with(−5)0,(−5)1,(−5)2,(−5)3,(−5)4,(−5)5,(−5)6 respectively.
Therefore, the actual coefficients are,
⇒(−5)0×1,(−5)1×6,(−5)2×15,(−5)3×20,(−5)4×15,(−5)5×6,(−5)6×1
Simplify the terms,
⇒1,−30,375,−2500,9375,−18750,15625
Hence, the expansion of (x−5)6 is x6−30x5+375x4−2500x3+9375x2−18750x+15625.
Note:
In binomial expansion, these coefficients are used in the form of combination where the expansion is
(x+a)n=nC0xna0+nC1xn−1a1+…+nCrxn−rar+…+nCn−1x1an−1+nCnx0an
The general coefficient value for (r+1)th term is nCr where nCn=r!(n−r)!n!.
