Question
Question: How do you evaluate the sine, cosine and tangent of the angle 225 degrees without using a calculator...
How do you evaluate the sine, cosine and tangent of the angle 225 degrees without using a calculator?
Solution
In order to solve the question we will require these formulas: sin(180o+θ)=−sin(θ),cos(180o+θ)=−cos(θ),tan(180o+θ)=tan(θ). Here we can clearly notice that the formulas of sine and cosine are negative but for tangent it is positive. This is because of the fact that the given angle 225o lies in the third quadrant. We will also use sin(45o)=21,cos(45o)=21,tan(45o)=1.
Complete step by step solution:
First we will discuss the definition of trigonometric functions, which is suitable for all trigonometric angles. One angle in any triangle, taken as a reference for trigonometric function, will be of 90o. The functions with those angles which bond both the sides of a triangle to that angle which is 90o together are called trigonometric functions. These trigonometric functions are sine, cosine, tangent, cotangent, secant and cosecant.
In reference to the given question, it is required to evaluate sin(225o),cos(225o),tan(225o). By looking at the graph below, we come to know that the angle 225o lies only in the third quadrant. In this quadrant, we have negative sine and cosine but positive tangent. Moreover, the reference angle can be 180o+θ. Therefore,
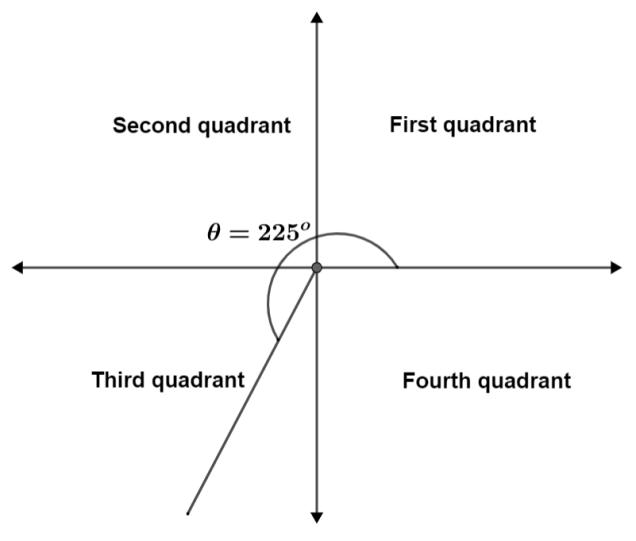
sin(225o)=sin(180o+45o)⇒sin(225o)=−sin(45o)(∵sin(180o+θ)=−sin(θ))⇒sin(225o)=−21(∵sin(45o)=21)
cos(225o)=cos(180o+45o)⇒cos(225o)=−cos(45o)(∵cos(180o+θ)=−cos(θ))⇒cos(225o)=−21(∵cos(45o)=21)
tan(225o)=tan(180o+45o)⇒tan(225o)=tan(45o)(∵tan(180o+θ)=tan(θ))⇒tan(225o)=1(∵tan(45o)=1)
Hence, the values of sin(225o)=−21,cos(225o)=−21,tan(225o)=1.
Note:
It is important where the given angle is lying. As there are four quadrants, the given angle can lie in any of these quadrants. In this question the angle 225o lies in the third quadrant. After this we can use the required formulas and complete the answer. We could have also used the reference angle as 270o−θ and solved it. For example, sin(225o)=sin(270o−45o) and solve it further as done above. One should remember all formulas related to trigonometric functions. As here it is required to use sin(45o)=21,cos(45o)=21,tan(45o)=1.
