Question

How do you evaluate the $\sin$, $\text{cosine}$ and $\text{tangent}$ of the angle $30$ degrees without using a calculator ?

Answer 1

This is the question on the topic of trigonometric function like sin, cosine and tangent of an angle. To solve this type of question we need to apply the function in terms of the distance of the sides of a right-angled triangle. One of the angles of the triangle is already given to find the value of the trigonometric function.

Complete step-by-step solution:
The question asks us to find the value of the trigonometric function $\sin$, $\text{cosine}$ and $\operatorname{tangent}$ of the angle $30$ degrees without using a calculator. This question will be solved by applying Pythagoras Theorem on the trigonometric function .As we know that Pythagoras theorem is applied in a right-angled triangle.
We know that $\sin$ of an angle refers to the perpendicular height by hypotenuse, mathematically which is represented by $\sin \theta =\dfrac{\text{perpendicular height}}{\text{hypotenuse}}$ , similarly $\cos$ of an angle refers to the base by hypotenuse, mathematically which is represented by $\cos \theta =\dfrac{\text{base}}{\text{hypotenuse}}$ and in the same manner $\text{tangent}$ of an angle refers to the perpendicular height by hypotenuse, mathematically which is represented by $\tan \theta =\dfrac{\text{perpendicular height}}{\text{base}}$.
If we consider a right-angled triangle with one of its angle as${{30}^{\circ }}$, where $AB$ is the hypotenuse, $BC$ is the perpendicular height and $AC$ is the base of the right angle triangle $ABC$ given below.

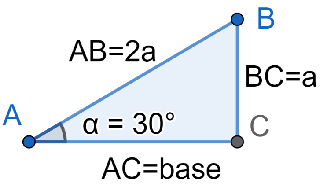
Now consider a right-angled triangle having height as $”a”$ and hypotenuse as $”2a”$. On using the formula to find $\sin$of an angle we get:
$\Rightarrow \sin\alpha =\dfrac{\text{BC}}{\text{AB}}$
$\Rightarrow \sin {{30}^{\circ }}=\dfrac{a}{2a}$
$\Rightarrow \sin {{30}^{\circ }}=\dfrac{1}{2}$
Using the Pythagoras theorem we will find the base of the triangle. The height and the hypotenuse is
$a$ and $2a$ respectively, so base is
$\Rightarrow \sqrt{{{\left( 2a \right)}^{2}}-{{\left( a \right)}^{2}}}$
$\Rightarrow \sqrt{4{{a}^{2}}-{{a}^{2}}}$
$\Rightarrow \sqrt{3{{a}^{2}}}$
$\Rightarrow \sqrt{3}a$
So the value of $\cos {{30}^{\circ }}$ becomes:
$\Rightarrow \cos \alpha = \dfrac{\text{AC}}{\text{AB}}$
$\Rightarrow \cos {{30}^{\circ }}=\dfrac{\sqrt{3}a}{2a}$
$\Rightarrow cos {{30}^{\circ }} = \dfrac{\sqrt{3}}{2}$
Now we will find the value for $\tan {{30}^{\circ }}$ using the formula
$\Rightarrow \tan \alpha =\dfrac{\text{BC}}{\text{AC}}$
$\Rightarrow \text{tan 3}{{0}^{\circ }}\text{=}\dfrac{a}{\sqrt{3}a}$
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
$\therefore$ The value of $\sin {{30}^{\circ }}=\dfrac{1}{2}$ , $\cos {{30}^{\circ}}=\dfrac{\sqrt{3}}{2}$ and $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ .

Note: We should know the formulas of these trigonometric functions. We can also find the values of the trigonometric function with the help of power series. The formula for sin x is:
$\sin x=x-\dfrac{{{x}^{3}}}{3!}+\dfrac{{{x}^{5}}}{5!}-\dfrac{{{x}^{7}}}{7!}+\dfrac{{{x}^{9}}}{9!}-................$
Similarly formula for cos x is:
$\cos x=1-\dfrac{{{x}^{2}}}{2!}+\dfrac{{{x}^{4}}}{4!}-\dfrac{{{x}^{6}}}{6!}+\dfrac{{{x}^{8}}}{8!}-.......................$
Here the angle $x$ is measured in terms of radians.