Solveeit Logo
Login

Question

Question: How do you evaluate the integral of \(\int{\dfrac{dx}{1+{{x}^{2}}}}\)from \(-1\) to \(1\) ?...

How do you evaluate the integral of ∫dx1+x2\int{\dfrac{dx}{1+{{x}^{2}}}}from −1-1 to 11 ?

Explanation

Solution

Integration is the summation of all the smaller parts. There are two types of integration. One is indefinite integration. This one doesn’t have limits that mean we don’t have a boundary for this. And the second one is definite integration. There are certain defined limits here. There is a lower limit and an upper limit. And we have to add or integrate only between these limits.

Complete step by step answer:
There is one key formula that we should know before starting our integration. And that is :
∫abf(x)dx=[F(x)]ab=F(a)−F(b)\int\limits_{a}^{b}{f\left( x \right)dx=\left[ F\left( x \right) \right]_{a}^{b}=F\left( a \right)-F\left( b \right)}
Where ff be a continuous function defined on the closed integral [a,b]\left[ a,b \right] and FF be an antiderivative of f.f.
Let us consider f(x)=11+x2f\left( x \right)=\dfrac{1}{1+{{x}^{2}}} .
11+x2\dfrac{1}{1+{{x}^{2}}} is surely continuous on [−1,1]\left[ -1,1 \right], and we can verify it from the below shown graph.

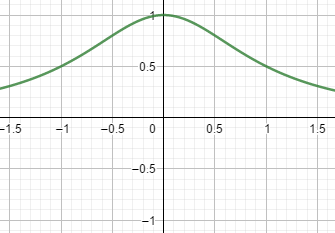
Now we are supposed to integrate this within (−1,1)\left( -1,1 \right) . We represent this in the following way :
⇒∫−11dx1+x2\Rightarrow \int\limits_{-1}^{1}{\dfrac{dx}{1+{{x}^{2}}}} .
Here −1-1 is called the lower limit and 11 is called the upper limit.
We know that :
∫dx1+x2=tan⁡−1x\int{\dfrac{dx}{1+{{x}^{2}}}={{\tan }^{-1}}x}.
We know this from our previous knowledge.
Now let’s do the same but after that, we should apply the limits.
Upon integrating, we get the following :
⇒∫−11dx1+x2 ⇒∫−11dx1+x2=[tan⁡−1x]−11 \begin{aligned} & \Rightarrow \int\limits_{-1}^{1}{\dfrac{dx}{1+{{x}^{2}}}} \\\ & \Rightarrow \int\limits_{-1}^{1}{\dfrac{dx}{1+{{x}^{2}}}}=\left[ {{\tan }^{-1}}x \right]_{-1}^{1} \\\ \end{aligned}
We know that tan⁡π4=1\tan \dfrac{\pi }{4}=1 . So we can say tan⁡−1(1)=π4{{\tan }^{-1}}\left( 1 \right)=\dfrac{\pi }{4} …..eqn(1)eqn\left( 1 \right)
And we also know that tan⁡(−π4)=−1\tan \left( -\dfrac{\pi }{4} \right)=-1 . So we can say tan⁡−1(−1)=−π4{{\tan }^{-1}}\left( -1 \right)=-\dfrac{\pi }{4} …..eqn(2)eqn\left( 2 \right)
Now let us make use of it eqn(1)&eqn(2)eqn\left( 1 \right)\And eqn\left( 2 \right) . Upon doing so, we get the following :
⇒tan⁡−1(1)−tan⁡−1(−1) ⇒π4−(−π4) ∴π2 \begin{aligned} & \Rightarrow {{\tan }^{-1}}\left( 1 \right)-{{\tan }^{-1}}\left( -1 \right) \\\ & \Rightarrow \dfrac{\pi }{4}-\left( -\dfrac{\pi }{4} \right) \\\ & \therefore \dfrac{\pi }{2} \\\ \end{aligned}
If the limits are not mentioned in the question and we are just asked to integrate it then just tan⁡−1x{{\tan }^{-1}}xwould be our answer. We don’t have to substitute the limits.

Hence, upon evaluating the integral ∫dx1+x2\int{\dfrac{dx}{1+{{x}^{2}}}} from −1-1 to 11 we get π2\dfrac{\pi }{2}.

Note: We have to be careful while integrating. Sometimes, we should also make use of some substitutions in order to make the sum easier. We should remember the properties of definite integrals and also the anti-derivatives of all the crucial functions.