Question

How do you evaluate the equation $\arctan (3)$ ?

Answer 1

Hint : In order to evaluate the value of $\arctan (3)$ , we need to know first what is $\arctan$ . $\arctan x$ is an angle whose tangent function is equal to $\dfrac{x}{1}$ . Equate $\arctan x$ with $\arctan (3)$ and put it in the value $\tan p = \tan \left( {\arctan x} \right)$ and solve for $p$ , where $p$ represents an angle opposite the perpendicular.

Complete step by step solution:
We are given $\arctan (3)$ .
Let $p = \arctan x$ , where $p$ represents an angle opposite the perpendicular.
The representing diagram of the following is:

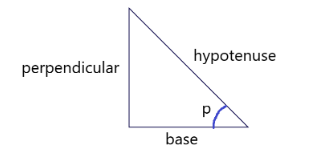
So, we can write it as:
$\tan p = \tan \left( {\arctan x} \right)$
As we know that $\arctan x$ is an angle whose tangent function is equal to $\dfrac{x}{1}$ .
So, from the previous equation we can write:
$\tan p = \tan \left( {\arctan x} \right) = \dfrac{x}{1}$
We are given with $\arctan (3)$ , so from the above equation we can write it as:
$\tan p = \tan \left( {\arctan 3} \right) = \dfrac{3}{1}$
Basically, we need to calculate $p$ which is the angle opposite perpendicular.
From above equation we can write:
$\tan \left( {\arctan 3} \right) = 3 \\\ \arctan 3 = {\tan ^{ - 1}}3 \;$
Since, we don’t know the value of ${\tan ^{ - 1}}3$ , so by using calculator we get that:
${\tan ^{ - 1}}3 = 71.565$ .
Since, we got $\tan p = \tan \left( {\arctan 3} \right)$ , placing the value of $\arctan 3 = {\tan ^{ - 1}}3$ and we get:
$\tan p = \tan \left( {{{\tan }^{ - 1}}3} \right)$
That implies $p = \left( {{{\tan }^{ - 1}}\left( 3 \right)} \right) = 71.565$ .
Therefore, The value of $\left( {\arctan 3} \right) = 71.565$ in degrees.
But, to write the value in radians multiply the value $\left( {\arctan 3} \right) = 71.565$ in degrees with $\dfrac{\pi }{{180}}$ and we get:
$\left( {\arctan 3} \right) = 71.565 \times \dfrac{\pi }{{180}}$ radians
On further solving we get:
$\left( {\arctan 3} \right) = 1.2490$ radians.
Therefore, The value of $\left( {\arctan 3} \right) = 1.2490$ in radians.
So, the correct answer is “1.2490 radians”.

Note :
i.It’s not compulsory to convert the value in radians until its not given in the question, we can leave at degree also.
ii.If some trigonometric values are not known to us for some different angles, then only calculators should be used.
iii.We could have done the question directly without taking $p$ , then also it would have given the same answer.