Question

How do you evaluate $\text{arccos}\left( \dfrac{1}{2} \right)$ without a calculator?

Answer 1

In the problem we need to calculate the value of angle where the $\cos$ trigonometric ratio gives the value $\dfrac{1}{2}$. For this we will assume the given value to a variable let’s say $x$. Now we will apply the $\cos$ trigonometric function on both sides of the equation. Now we will apply the exponential rules and calculate the value of $\cos x$. After getting the value of $\cos x$ we will observe the trigonometric circle and we will write the required result.

Complete step by step solution:
Given that, $\text{arccos}\left( \dfrac{1}{2} \right)$.
Arc is the function which is normally represented by an inverse function. So, we can write $\text{arccos}\left( \dfrac{1}{2} \right)$ as ${{\cos }^{-1}}\left( \dfrac{1}{2} \right)$.
Let us assume the above value with a variable say $x$. Then we can write
$x={{\cos }^{-1}}\left( \dfrac{1}{2} \right)$
Applying the $\cos$ trigonometric function on both sides of the above equation, then we will get
$\cos x=\cos \left( {{\cos }^{-1}}\left( \dfrac{1}{2} \right) \right)$
We know that when we multiply an inverse function to the original function then we will get unity as a result. Now the above equation is modified as
$\cos x=\dfrac{1}{2}$
From the trigonometric circle which is shown below, we can write the value of $x$ as $60{}^\circ$.

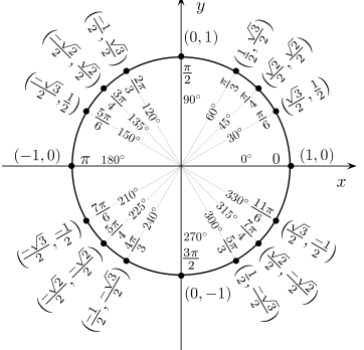
Hence the final value of $\text{arccos}\left( \dfrac{1}{2} \right)$ is $60{}^\circ$.

Additional Information:
From the above-mentioned trigonometric circle we can find any trigonometric ratio value for the given angle by using the basic trigonometric formulas like
$\tan x=\dfrac{\sin x}{\cos x}$, $\sec x=\dfrac{1}{\cos x}$, $\csc x=\dfrac{1}{\sin x}$, $\cot x=\dfrac{1}{\tan x}$

Note:
In the question they have asked to don’t use the calculator because if you used the calculator to find the value, then we will get the solution in a single step which is not advisable in any examinations.