Question

How do you evaluate $\tan \left( {\dfrac{{ - 7\pi }}{4}} \right)?$

Answer 1

We need to know the trigonometric table values and basic definitions $\tan \theta$ . We need to know the value of $\cos \left( {\dfrac{{ - 7\pi }}{4}} \right)$ and $\sin \left( {\dfrac{{ - 7\pi }}{4}} \right)$ .

This question involves the operation of addition/ subtraction/ multiplication/ division. Also, we need to know the degree value of $\pi$ terms. By having the value of $\sin \theta$ and $\cos \theta$ we can easily find out the value of $\tan \theta$ .

Complete step by step solution:
The given question is shown below
$\tan \left( {\dfrac{{ - 7\pi }}{4}} \right) = ?$ $\to \left( 1 \right)$
To solve the above equation we need to know the basic definition $\tan \theta$ .

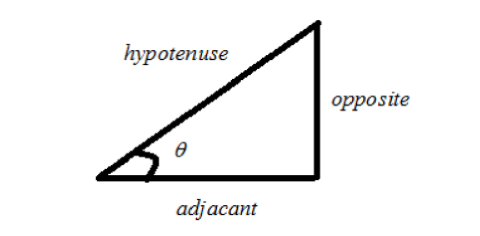
The above figure is used to define the $\tan \theta$ according to the position of $$\theta

So, we get $$\tan \theta = \dfrac{{opposite}}{{adjacant}} \to \left( 2 \right)$$ Also, we get the definition for $$\sin \theta $$ and $$\cos \theta $$ from the figure mentioned above. We get, $$\sin \theta = \dfrac{{opposite}}{{hypotenuse}}$$ $$ \to \left( 3 \right)$$ And, $$\cos \theta = \dfrac{{adjacant}}{{hypotenuse}}$$ $$ \to \left( 4 \right)$$ Let’s divide the equation $$\left( 3 \right)$$ by the equation $$\left( 4 \right)$$ we get, $$\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{\left( {\dfrac{{opposite}}{{hypotenuse}}} \right)}}{{\left( {\dfrac{{adjacant}}{{hypotenuse}}} \right)}}$$ The above equation can also be written as, $$\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{opposite}}{{hypotenuse}} \times \dfrac{{hypotenuse}}{{adjacant}}$$ $$\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{opposite}}{{adjacant}} \to \left( 5 \right)$$ By comparing the equation $$\left( 5 \right)$$ and $$\left( 2 \right)$$ , we get

\left( 2 \right) \to \tan \theta = \dfrac{{opposite}}{{adjacant}} \\
\left( 5 \right) \to \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{opposite}}{{adjacant}} \\

So, $$\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} \to \left( 6 \right)$$ We know that the value $$\theta $$ is $$\left( {\dfrac{{ - 7\pi }}{4}} \right)$$ (Given in the question). From the trigonometric table value,

\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }} \\
\cos \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }} \\

So, $$\sin \left( {\dfrac{\pi }{4}} \right) = \cos \left( {\dfrac{\pi }{4}} \right)$$ From the above equations, we get, $$\sin \left( {\dfrac{{ - 7\pi }}{4}} \right) = \cos \left( {\dfrac{{ - 7\pi }}{4}} \right)$$ $$ \to \left( 7 \right)$$ Let’s substitute the above equation in the equation $$\left( 6 \right)$$ , we get $$\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$$ $$\tan \left( {\dfrac{{ - 7\pi }}{4}} \right) = \dfrac{{\left( {\sin \dfrac{{ - 7\pi }}{4}} \right)}}{{\left( {\cos \dfrac{{ - 7\pi }}{4}} \right)}}$$ $$\tan \left( {\dfrac{{ - 7\pi }}{4}} \right) = 1$$ **So, the final answer is, The value of $$\tan \left( {\dfrac{{ - 7\pi }}{4}} \right)$$ is $$1$$ .** **Note:** In these types of questions we would remember the trigonometric table values and basic definitions of $$\sin \theta ,\cos \theta $$ and $$\tan \theta $$ .Note that when $$\dfrac{\pi }{4}$$ is involved in $$\theta $$ value, the value of $$\tan \theta $$ is always $$1$$ . When we have the fraction term in the denominator, the fraction term of the denominator will come to the position of the numerator. If we have a fraction term in the numerator, the denominator of the fraction term will come to the position of the denominator as follows, $$\dfrac{{\left( {\dfrac{x}{y}} \right)}}{{\left( {\dfrac{z}{l}} \right)}} = \left( {\dfrac{x}{y} \times \dfrac{l}{z}} \right)$$