Question

How do you evaluate $\tan \left( {{\cos }^{-1}}\left( -\dfrac{2}{3} \right) \right)$ without a calculator?

Answer 1

In this question we need to calculate the value of the given expression without using a calculator. We can observe that the given expression consists of two trigonometric identities out of them one is the inverse trigonometric identity. So, we will first consider the inverse trigonometric identity and try to form the triangle using basic trigonometric definitions. After that we will calculate all the sides of the triangle by using Pythagoras theorem and then we can calculate the whatever trigonometric value from the triangle.

Complete step by step solution:
Given that, $\tan \left( {{\cos }^{-1}}\left( -\dfrac{2}{3} \right) \right)$.
Let us assume $x={{\cos }^{-1}}\left( -\dfrac{2}{3} \right)$.
Apply $\cos$ function on both sides of the above equation, then we will get
$\begin{aligned} & \Rightarrow \cos \left( x \right)=\cos \left( {{\cos }^{-1}}\left( -\dfrac{2}{3} \right) \right) \\\ & \Rightarrow \cos x=-\dfrac{2}{3} \\\ \end{aligned}$
In the above equation we have the value of $\cos x$ as negative. So that angle $x$ lies in the second quadrant. We know that the value of $\tan x$ will be negative for $x$ in the second quadrant.
We know that the basic definition of the trigonometric ratio $\cos x$ will be
$\begin{aligned} & \Rightarrow \cos x=\dfrac{\text{Adjacent side to }x}{\text{Hypotenuse}} \\\ & \Rightarrow \dfrac{2}{3}=\dfrac{\text{Adjacent side to }x}{\text{Hypotenuse}} \\\ \end{aligned}$
From the above equation we can assume a triangle as shown in below

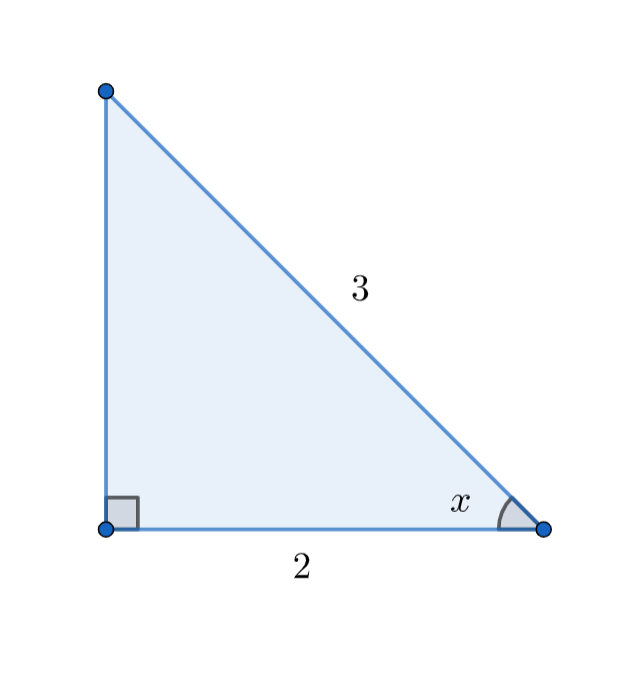
From the Pythagoras theorem, in the above triangle we can write
$\begin{aligned} & \Rightarrow \text{opposite sid}{{\text{e}}^{2}}+{{2}^{2}}={{3}^{2}} \\\ & \Rightarrow \text{opposite sid}{{\text{e}}^{2}}=9-4 \\\ & \Rightarrow \text{opposite side}=\sqrt{5} \\\ \end{aligned}$
Now the triangle will be

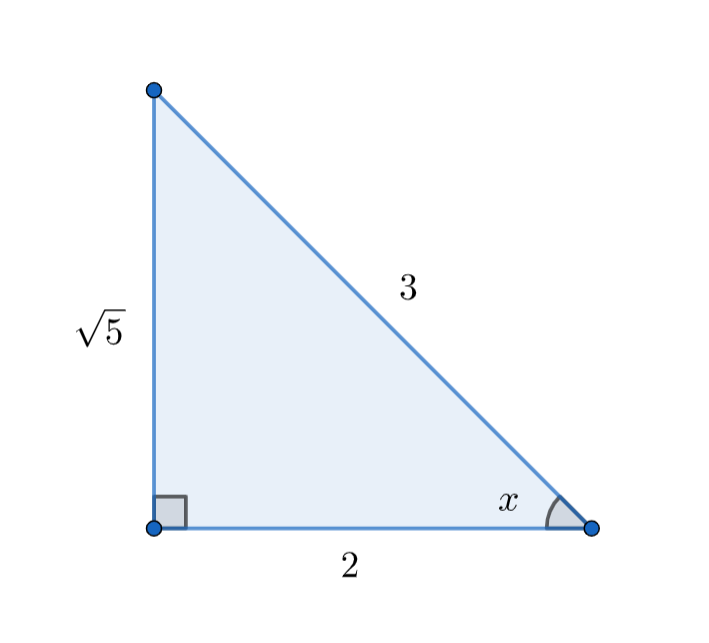
In the above triangle we can write the value of $\tan x$ as
$\begin{aligned} & \Rightarrow \tan x=\dfrac{\text{opposite side to }x}{\text{adjacent side to }x} \\\ & \Rightarrow \tan x=\dfrac{\sqrt{5}}{2} \\\ \end{aligned}$
But the angle $x$ lies in the second quadrant hence the value of $\tan x$ will be
$\Rightarrow \tan x=-\dfrac{\sqrt{5}}{2}$
Substituting our assumption $x={{\cos }^{-1}}\left( -\dfrac{2}{3} \right)$ in the above equation, then we will get
$\Rightarrow \tan \left( {{\cos }^{-1}}\left( -\dfrac{2}{3} \right) \right)=-\dfrac{\sqrt{5}}{2}$

Note: For this problem we can also directly calculate the value in another method. After getting the value $\cos x=-\dfrac{2}{3}$, we will calculate the value of $\sin x$ from the trigonometric identity ${{\sin }^{2}}x+{{\cos }^{2}}x=1$.
$\begin{aligned} & \Rightarrow \sin x=\sqrt{1-{{\cos }^{2}}x} \\\ & \Rightarrow \sin x=\sqrt{1-{{\left( -\dfrac{2}{3} \right)}^{2}}} \\\ & \Rightarrow \sin x=\sqrt{1-\dfrac{4}{9}} \\\ & \Rightarrow \sin x=\sqrt{\dfrac{9-4}{9}} \\\ & \Rightarrow \sin x=\dfrac{\sqrt{5}}{3} \\\ \end{aligned}$
From this value we can write the value of $\tan x$ as
$\begin{aligned} & \Rightarrow \tan x=\dfrac{\sin x}{\cos x} \\\ & \Rightarrow \tan x=\dfrac{\dfrac{\sqrt{5}}{3}}{-\dfrac{2}{3}} \\\ & \Rightarrow \tan x=-\dfrac{\sqrt{5}}{2} \\\ \end{aligned}$
From both the methods we got the same result.