Question

How do you evaluate $\tan \dfrac{\pi }{3}$ ?

Answer 1

To solve the given question, first we need to know about the fact that $\pi$ radians is equal to ${{180}^{\circ }}$. Then solve the question by calculating as $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ , taking $\theta =\dfrac{\pi }{3}$. Then we continue by finding the sin and cos of the same angle as given and get the exact value of $\tan \dfrac{\pi }{3}$.

Formula used:
$\pi$ radian = ${{180}^{\circ }}$
To find the tangent of any angle we need to just divide the sine and cosine of the same angle:$\tan \theta =\dfrac{\sin \theta }{\cos \theta }=\dfrac{perpendicular}{base}$

Complete step by step solution:
Let us consider the triangle ABC right angled at B

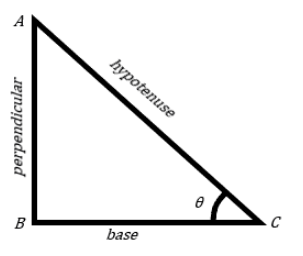
We know that:
$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$, where

$$\sin \theta =\dfrac{perpendicular}{hypotenuse} \\\ \Rightarrow\cos \theta =\dfrac{base}{hypotenuse} \\\$$

Now if we divide $\sin \theta$ by $\cos \theta$,, we will get
$\dfrac{\sin \theta }{\cos \theta }=\dfrac{\dfrac{perpendicular}{hypotenuse}}{\dfrac{base}{hypotenuse}}=\dfrac{perpendicular}{base}$
Hence we get the relation between sin, cos and tan,
$\tan \theta =\dfrac{\sin \theta }{\cos \theta }=\dfrac{perpendicular}{base}$
Now the next step is to find the value of $\dfrac{\pi }{3}$,
As we know that,
$\pi$ radian = ${{180}^{0}}$
Therefore, $\dfrac{\pi }{3}=\dfrac{{{180}^{0}}}{3}={{60}^{0}}$
Now putting $\dfrac{\pi }{3}={{60}^{0}}$
$\tan {{60}^{0}}=\dfrac{\sin {{60}^{0}}}{\cos {{60}^{0}}}$
From the trigonometric table we know the value of
$\sin {{60}^{0}}=\dfrac{\sqrt{3}}{2}$ and $\cos {{60}^{0}}=\dfrac{1}{2}$
$\therefore\tan {{60}^{\circ }}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}}=\dfrac{\sqrt{3}}{1}=\sqrt{3}$

Therefore, the value of $\tan \dfrac{\pi }{3}=\sqrt{3}$.

Note: One must be careful while noted down the values from the trigonometric table to avoid any error in the answer. We must know the basic value of sine and cosine of the angles like ${{0}^{\circ }}$, ${{30}^{\circ }}$, ${{60}^{\circ }}$, ${{90}^{\circ }}$ etc.Whenever we get this type of problem, first convert the radians to degrees to make the process of solving the question easier. The sine, cosine and the tangent are the three basic functions in introduction to trigonometry which shows the relation between all the sides of the triangles.