Question

How do you evaluate sine, cosine, tangent of $\dfrac{\pi }{4}$ without using a calculator?

Answer 1

In the above question, is based on the concept of trigonometry. The sine, cosine, tangent functions can be solved by solving the relationship between angles and sides of the triangle.

Using $\dfrac{\pi }{4}$ as the angle we can find the length of sides to get the value of each function.

Complete step by step solution:
Given is the angle which is $\dfrac{\pi }{4}$ or ${45^ \circ }$.So to solve the value of functions, we
need to know that one angle in the triangle is always ${90^ \circ }$.Since we want to find the function for the angle for ${45^ \circ }$,so the other angle in the triangle is ${45^ \circ }$.

The total angle of triangle is ${180^ \circ }$.Therefore by adding two angles and subtracting it with
${180^ \circ }$ we get a third angle.
${180^ \circ } - ({90^ \circ } + {45^ \circ }) = {45^ \circ }$.

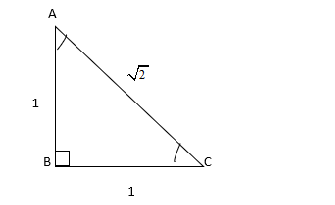
So, we consider the unit triangle $\vartriangle ABC$where two sides are equal. Since the two sides of triangles are equal, the triangle is an isosceles triangle. Therefore, by applying Pythagoras theorem, we
get $AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2$

Now, we have to apply the trigonometric properties for different functions. For sine function the formula is the opposite side divided by hypotenuse.
$\sin {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$

For cosine function, the formula is adjacent side divided by hypotenuse. Therefore, we get
$\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$

For tangent function, the formula is sine function divided by cosine function. $$$$
$\tan {45^ \circ } = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}} = 1$

Therefore, we get the above values.

**Note:****An important thing to note is that $\dfrac{1}{{\sqrt 2 }}$ can also be further solved to get a decimal numbers.So, rationalizing it with $\sqrt 2$,we get $\dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}$.The value of $\sqrt 2$is 1.414,therefore dividing it by 2 we get
0.707.