Question

How do you evaluate $\sin (\arctan (\dfrac{3}{4}))$ without a calculator?

Answer 1

Hint : We have Pythagoras theorem to find out the relation between the sides of a right-angled triangle but to find out the relation between the sides of the right-angled triangle and its angles, we use trigonometry. There are six trigonometric functions; sine, cosine, tangent, cosecant, secant and cotangent functions. These functions are given as the ratio of two sides of the right angles triangle.

Complete step-by-step answer :
In the given question, we have to evaluate $\sin (\arctan (\dfrac{3}{4}))$ , sine of $\arctan \theta$ means the sine of the angle whose tangent is $\theta$ . Thus, we have to find the sine of the angle whose tangent is $\dfrac{3}{4}$ , we know that $\tan \theta = \dfrac{3}{4}$ .

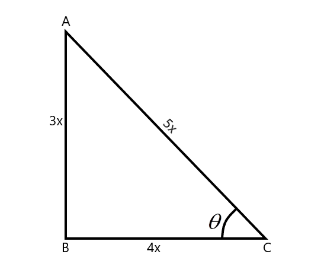
We are given that $\tan \theta = \dfrac{3}{4}$
We know that $\tan \theta = \dfrac{{perpendicular}}{{base}}$
On comparing the above equations, we get $\dfrac{{perpendicular}}{{base}} = \dfrac{3}{4}$
So, $perpendicular = 3x$ and $base = 4x$
Now, according to the Pythagoras theorem,
$hypotenuse = \sqrt {perpendicula{r^2} + bas{e^2}} \\\ \Rightarrow hypotenuse = \sqrt {{{(3x)}^2} + {{(4x)}^2}} = \sqrt {9{x^2} + 16{x^2}} = \sqrt {25{x^2}} \\\ \Rightarrow hypotenuse = \pm 5x \\\$
$\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}} = \dfrac{{3x}}{{ \pm 5x}} \\\ \Rightarrow \sin \theta = \pm \dfrac{3}{5} \;$
Hence, $\sin (arc\tan (\dfrac{3}{4}))$ is equal to $\pm \dfrac{3}{5}$
So, the correct answer is “ $\pm \dfrac{3}{5}$ ”.

Note : We know trigonometric functions are the ratio of sides of a right-angled triangle; sine function is the ratio of the perpendicular and the hypotenuse, thus we have to find the value of hypotenuse to find out the value of the sine function, we also know that tangent function is the ratio of the perpendicular and the base of a right-angled triangle, as we know the value of the tangent function, we can find out the value of the sides of the right-angled triangle and thus the correct answer.