Question

How do you evaluate $\sin {30^ \circ }$ ?

Answer 1

Hint : We will find the value of this trigonometric function and the angle $\sin {30^ \circ }$ using an equilateral triangle. Equilateral triangle has all angles the same and all sides are of the same length. We will divide the equilateral triangle such that we get a ${30^ \circ } - {60^ \circ } - {90^ \circ }$ triangle. Using that and the ratio of trigonometric identity $\sin \theta$ we will find the value of $\sin {30^ \circ }$ .

Complete step-by-step answer :
Let first draw an equilateral triangle.

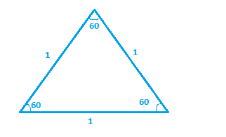
Now we will divide this triangle exactly half.

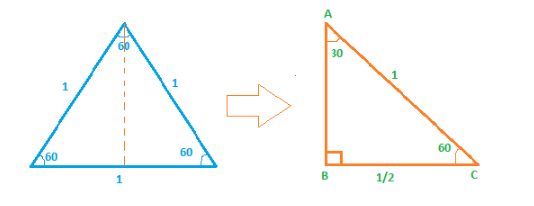
Now consider the second triangle obtained after division ∆ABC.
In that we can observe all the three angles.
Now we know that sin function is the ratio of opposite sides to that hypotenuse.
${{sin\theta = }}\dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$
Now we will check this for the triangle we obtained,
$\sin {30^ \circ } =\dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$
The side opposite to ${\text{3}}{0^ \circ }$ is BC and the hypotenuse is AC. Putting these in the ratios,
$\sin {30^ \circ } =\dfrac{{{\text{BC}}}}{{{\text{AC}}}}$
Then substitute their numerical values,
$\sin {30^ \circ } =\dfrac{{\dfrac{1}{2}}}{{\text{1}}}$
On solving we get,
$\sin {30^ \circ } =\dfrac{1}{2}$
This is the value of the function $\sin {30^ \circ }$
So, the correct answer is “ $\dfrac{1}{2}$ ”.

Note : We can also find the other ratios with the same method. But if we need an adjacent side for any ratio or the side that is not known right now we will find it with the help of Pythagoras theorem. That side AB is $\dfrac{{\sqrt 3 }}{2}$ . Now we can go for functions of ${60^ \circ }$ also. Note that we have not taken the isosceles triangle because we cannot obtain the required angle with the help of that.