Question
Question: How do you evaluate \[\sec \left( {{\tan }^{-1}}8 \right)\] without a calculator?...
How do you evaluate sec(tan−18) without a calculator?
Solution
We explain the function arctan(x). We express the inverse function of tan in the form of arctan(x)=tan−1x. We draw the graph of arctan(x) and the line x=8 to find the intersection point. Thereafter we take the sec ratio of that angle to find the solution. We also use the representation of a right-angle triangle with height and base ratio being 8 and the angle being θ.
Complete step-by-step solution:
The internal part tan−18 of sec(tan−18) is an angle. We assume tan−18=θ.
This gives in ratio tanθ=8. We know tanθ=baseheight.
We can take the representation of a right-angle triangle with height and base ratio being 8 and the angle being θ. The height and base were considered with respect to that particular angle θ.
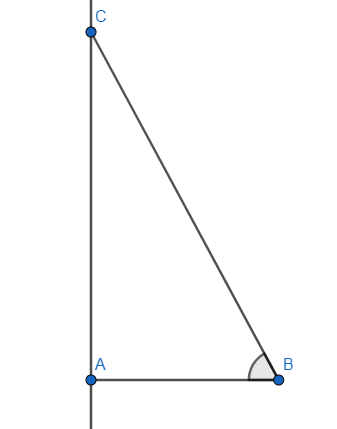
In this case we take AB=x and keeping the ratio in mind we have AC=8x as the ratio has to be 8.
Now we apply the Pythagoras’ theorem to find the length of BC. BC2=AB2+AC2.
So, BC2=x2+(8x)2=65x2 which gives BC=65x.
We need to find sec(tan−18) which is equal to secθ.
This ratio gives secθ=basehypotenuse. So, secθ=ABBC=x65x=65.
Therefore, sec(tan−18) is equal to 65.
Note: We can also apply the trigonometric image form to get the value of sec(tan−18).
It’s given that tanθ=8 and we need to find secθ. We know secθ=1+tan2θ.
Putting the values, we get secθ=1+tan2θ=1+82=65.
