Question

How do you evaluate $\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$ without a calculator?

Answer 1

We are asked to find the value of $\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$. There are two trigonometric functions. First find the value of cosine and then use this value to find the value of secant. Recall the relation between cosine and secant function and apply this relation.

Complete step by step solution:
We are asked to evaluate $\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$ without using calculator.
We have, $\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$.
Let us take, ${\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right) = \theta$ ……………....(i)
$\Rightarrow \left( {\dfrac{1}{2}} \right) = \cos \theta$
$\Rightarrow \cos \theta = \dfrac{1}{2}$
We know that secant is inverse of cosine, that is we can write
$\sec \theta = \dfrac{1}{{\cos \theta }}$
Putting the value of $\cos \theta$ we get,
$\sec \theta = \dfrac{1}{{\left( {\dfrac{1}{2}} \right)}}$
$\Rightarrow \sec \theta = 2$......................(ii)
Now, putting the value of $\theta$ from equation (i) we get,
$\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right) = 2$
Therefore, the value of $\sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$ is $2$

Alternative method:
Let $A = \sec \left( {{{\cos }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)$.
And let us take, ${\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right) = \theta$
$\Rightarrow \cos \theta = \dfrac{1}{2}$ …………………(iii)
Cosine of an angle can be written in terms of base and hypotenuse of a right angled triangle that is,

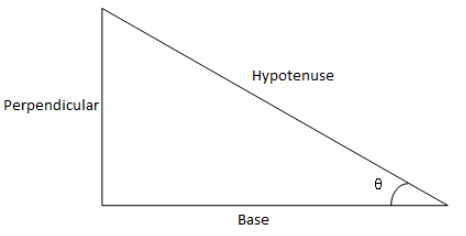
$\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$ ………………....(iv)
That means cosine of an angle is the ratio of base and hypotenuse of a right angled triangle.
We have,
$\cos \theta = \dfrac{1}{2}$
Comparing with equation (iv) we get,
$\dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{1}{2}$ ………………(v)

We can write secant as inverse of cosine, that is,
$\sec \theta = \dfrac{1}{{\cos \theta }}$
Putting the value of $\cos \theta$ from equation (iv) we get,
$\sec \theta = \dfrac{1}{{\left( {\dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}} \right)}}$
Putting the value of $\dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$ from equation (v) we get,
$\sec \theta = \dfrac{1}{{\left( {\dfrac{1}{2}} \right)}}$
$\therefore \sec \theta = 2$

Note: There are three main functions in trigonometry, these are sine, cosine and tangent. There are three other trigonometric functions which can be written in terms of the main functions, these are cosecant which is inverse of sine, secant which is inverse of cosine and cotangent which is inverse of tangent. Also, while solving questions related to trigonometry, you should always remember the basic trigonometric identities.