Question

How do you evaluate $\cot \left( \arctan \left( \dfrac{3}{5} \right) \right)$?

Answer 1

We explain the function $arc\tan \left( x \right)$. We express the inverse function of tan in the form of $arc\tan \left( x \right)={{\tan }^{-1}}x$. We draw the graph of $arc\tan \left( x \right)$ and the line $x=\dfrac{3}{5}$ to find the intersection point. Thereafter we take the cot ratio of that angle to find the solution.

Complete step by step answer:
The given expression is the inverse function of trigonometric ratio tan.
The arcus function represents the angle which on ratio tan gives the value.
So, $arc\tan \left( x \right)={{\tan }^{-1}}x$. If $arc\tan \left( x \right)=\alpha$ then we can say $\tan \alpha =x$.
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi$.
The general solution for that value where $\tan \alpha =x$ will be $n\pi +\alpha ,n\in \mathbb{Z}$.
But for $arc\tan \left( x \right)$, we won’t find the general solution. We use the principal value. For ratio tan we have $-\dfrac{\pi }{2}\le arc\tan \left( x \right)\le \dfrac{\pi }{2}$.
The graph of the function is

We now place the value of $x=\dfrac{3}{5}$ in the function of $arc\tan \left( x \right)$.
Let the angle be $\theta$ for which $arc\tan \left( \dfrac{3}{5} \right)=\theta$. This gives $\tan \theta =\dfrac{3}{5}$.
For this we take the line of $x=\dfrac{3}{5}$ and see the intersection of the line with the graph $arc\tan \left( x \right)$.

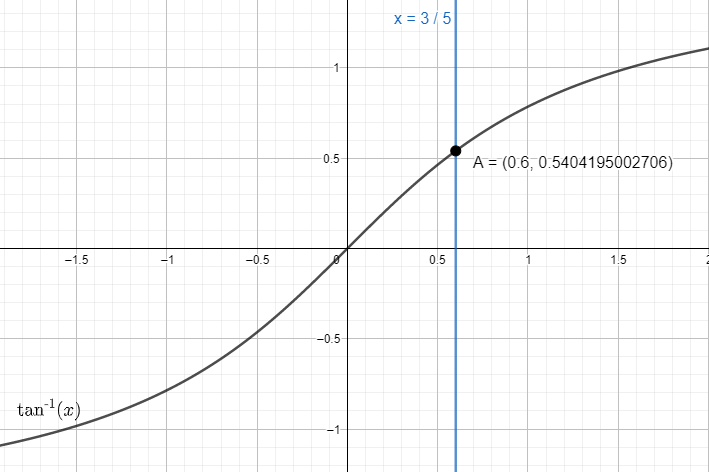
Putting the value in the graph of $arc\tan \left( x \right)$, we get $\theta =30.96$. (approx.)
We get the value of y coordinates as ${{30.96}^{\circ }}$.
Now we take $\cot \left( \arctan \left( \dfrac{3}{5} \right) \right)=\cot \left( {{30.96}^{\circ }} \right)=\dfrac{5}{3}$.

Therefore, the value of $\cot \left( \arctan \left( \dfrac{3}{5} \right) \right)$ is $\dfrac{5}{3}$.

Note: We can also apply the trigonometric identity where $\cot \theta =\dfrac{1}{\tan \theta }$. Also, in the exact solution domain of $-\dfrac{\pi }{2}\le \theta \le \dfrac{\pi }{2}$, $\tan \left( {{\tan }^{-1}}x \right)=x$.using those identities we get
$\cot \left( \arctan \left( \dfrac{3}{5} \right) \right)=\dfrac{1}{\tan \left( {{\tan }^{-1}}\left( \dfrac{3}{5} \right) \right)}=\dfrac{1}{\dfrac{3}{5}}=\dfrac{5}{3}$.