Question

How do you evaluate $\cos \left( \dfrac{2\pi }{9} \right)$?

Answer 1

We first assume a variable for $\cos \left( \dfrac{2\pi }{9} \right)$. We assume the concept of associative angle to find the value of $\cos \left( \dfrac{2\pi }{3} \right)$. Then using the formula of multiple angles of $\cos 3\alpha =4{{\cos }^{3}}\alpha -3\cos \alpha$, we get a cubic equation of $\cos \left( \dfrac{2\pi }{9} \right)=x$. We put the equation in the graph and find the solution as the approximate value.

Complete step by step solution:
We have to evaluate $\cos \left( \dfrac{2\pi }{9} \right)$. Let us assume that $\cos \left( \dfrac{2\pi }{9} \right)=x$.
Now we try to find the value of $\cos \left( \dfrac{2\pi }{3} \right)$. We use the concept of associative angle and get
$\cos \left( \dfrac{2\pi }{3} \right)=\cos \left( \pi -\dfrac{\pi }{3} \right)=-\cos \left( \dfrac{\pi }{3} \right)=-\dfrac{1}{2}$.
Now we use the multiple angle formula where $\cos 3\alpha =4{{\cos }^{3}}\alpha -3\cos \alpha$.
We put the value of $\alpha =\dfrac{2\pi }{9}$ and get
$\begin{aligned} & \cos \left( 3\times \dfrac{2\pi }{9} \right)=4{{\cos }^{3}}\left( \dfrac{2\pi }{9} \right)-3\cos \left( \dfrac{2\pi }{9} \right) \\\ & \Rightarrow \cos \left( \dfrac{2\pi }{3} \right)=4{{\left[ \cos \left( \dfrac{2\pi }{9} \right) \right]}^{3}}-3\left[ \cos \left( \dfrac{2\pi }{9} \right) \right] \\\ & \Rightarrow 4{{x}^{3}}-3x=-\dfrac{1}{2} \\\ \end{aligned}$
We now have to solve the cubic equation to find the value for $\cos \left( \dfrac{2\pi }{9} \right)=x$.
The simplified form of the equation is $8{{x}^{3}}-6x+1=0$.
We now try to plot the equation in the graph

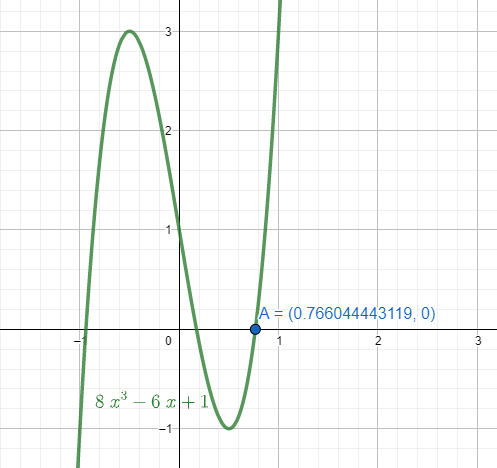
The value should be close to the value of $\cos \left( {{45}^{\circ }} \right)$ as $\cos \left( \dfrac{2\pi }{9} \right)=\cos \left( {{40}^{\circ }} \right)$. The graph intersects the line $y=0$ at two positive points and the closet one to $\cos \left( {{40}^{\circ }} \right)$ is $\cos \left( \dfrac{2\pi }{9} \right)=x=0.766$.
Therefore, the value of $\cos \left( \dfrac{2\pi }{9} \right)$ is $0.766$.

Note: We need to remember that the negative value of intersection of the equation in the graph is not valid as the quadrant for $\cos \left( \dfrac{2\pi }{9} \right)=x$ is first quadrant. Therefore, all the values of ratio cos are positive in the domain of $\left[ 0,\dfrac{\pi }{2} \right]$.